Open Middle®
Directions: Using the digits 0 to 9 at most one time each, fill in the boxes to create at least two different examples where the quotient is undefined.
Hint
What does undefined mean?
What operation could produce undefined values?
What operation could produce undefined values?
Answer
You can put any number instead of the #
Source: Daniel Luevanos
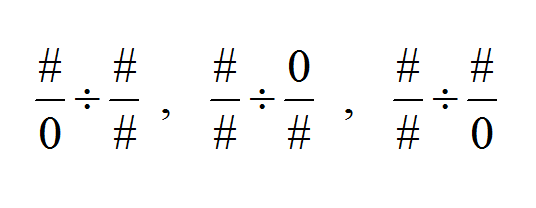
I think the third solution is wrong. When you invert the divisor #/0, it becomes 0/# so you have #/# x 0/# which is zero, not “undefined”.
I understand your reasoning, Patsy, but I don’t know if I would agree with you that the third solution is wrong.
Let’s imagine that we look at the example “4/5 divided by 3/0”. There are a two ways that I might interpret this question:
1.) We could think of the fractions as decimals. In doing so, we could interpret this example as “0.8 divided by undefined” which would lead to a result of undefined.
2.) We could think of the example as “4 divided by 5 divided by 3 divided by 0” which would have a result of undefined.
3.) Just to check my work, I typed the question in a calculator and the message “Cannot divide by zero” popped up.
I just checked your example in https://www.desmos.com/scientific and the answer was 0. I also checked in the google calculator and the answer is also, 0.
I can’t explain why other than you will end up multiplying 4/5 times 0/3, which is 0. When you type it into a calculator (4/5)/(3/0) is different than (4/5/3/0).
I see your point with the “wouldn’t that just be (4/5) divided by (UND)” I’m sure someone somewhere has a great explanation of why this is 0, but unfortunately it’s not me 🙂
Just a typo…”quotient” is spelled incorrectly in the directions.
Thanks for being a great resource for interesting math problems!
Fixed. Keep ’em coming. We all benefit from tightening them up.
In the case of #/0 ÷ #/#, there are 9*8*7 = 504 ways of putting three numbers between 1 and 9 in the spots with a #. Same goes for the cases #/# ÷ 0/# and #/# ÷ 0/#, so in total there are 504*3 = 1,512 solutions.