Directions: Use the digits 1-9, at most one time each, to fill the blanks.
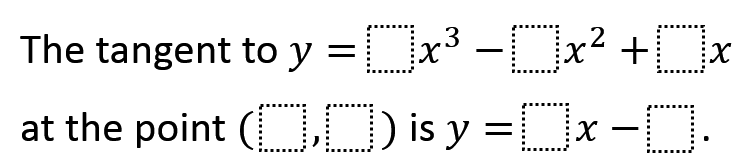
Hint
Which numbers can be large? Which must be fairly small?
Answer
Two possible answers are:
The tangent to 𝑦=4𝑥^3−5𝑥^2+7𝑥 at the point (1, 6) is 𝑦=9𝑥−3
The tangent to 𝑦=3𝑥^3−4𝑥^2+6𝑥 at the point (1, 5) is 𝑦=7𝑥−2
The tangent to 𝑦=4𝑥^3−5𝑥^2+7𝑥 at the point (1, 6) is 𝑦=9𝑥−3
The tangent to 𝑦=3𝑥^3−4𝑥^2+6𝑥 at the point (1, 5) is 𝑦=7𝑥−2
There may well be others.
Source: Catriona Shearer
 Open Middle®
Open Middle®

I have found 17 solutions (with a bit of python code). They are:
a = 3 b = 4 c = 6 // p = 1 q = 5 // m = 7 n = 2 ** see answer
a = 3 b = 4 c = 7 // p = 1 q = 6 // m = 8 n = 2
a = 3 b = 4 c = 8 // p = 1 q = 7 // m = 9 n = 2
a = 3 b = 5 c = 8 // p = 1 q = 6 // m = 7 n = 1
a = 4 b = 5 c = 7 // p = 1 q = 6 // m = 9 n = 3 ** see answer
a = 4 b = 7 c = 5 // p = 1 q = 2 // m = 3 n = 1
a = 4 b = 7 c = 8 // p = 1 q = 5 // m = 6 n = 1
a = 5 b = 4 c = 2 // p = 1 q = 3 // m = 9 n = 6
a = 5 b = 7 c = 8 // p = 1 q = 6 // m = 9 n = 3
a = 5 b = 8 c = 4 // p = 1 q = 1 // m = 3 n = 2
a = 5 b = 8 c = 7 // p = 1 q = 4 // m = 6 n = 2
a = 6 b = 7 c = 4 // p = 1 q = 3 // m = 8 n = 5
a = 6 b = 8 c = 3 // p = 1 q = 1 // m = 5 n = 4
a = 6 b = 8 c = 5 // p = 1 q = 3 // m = 7 n = 4
a = 6 b = 8 c = 7 // p = 1 q = 5 // m = 9 n = 4
a = 7 b = 8 c = 4 // p = 1 q = 3 // m = 9 n = 6
a = 1 b = 5 c = 7 // p = 3 q = 3 // m = 4 n = 9
(numbers in respective order)
And here four more. Due to a coding error I had missed them before.
a = 3 b = 5 c = 9 // p = 1 q = 7 // m = 8 n = 1
a = 5 b = 9 c = 6 // p = 1 q = 2 // m = 3 n = 1
a = 5 b = 9 c = 7 // p = 1 q = 3 // m = 4 n = 1
a = 7 b = 9 c = 3 // p = 1 q = 1 // m = 6 n = 5
Not all of them are correct, because repetitions have gone unnoticed. But 11 of them are “clean” (hopefully):
a = 3 b = 4 c = 6 // p = 1 q = 5 // m = 7 n = 2
a = 3 b = 4 c = 7 // p = 1 q = 6 // m = 8 n = 2
a = 3 b = 4 c = 8 // p = 1 q = 7 // m = 9 n = 2
a = 4 b = 5 c = 7 // p = 1 q = 6 // m = 9 n = 3
a = 5 b = 4 c = 2 // p = 1 q = 3 // m = 9 n = 6
a = 5 b = 7 c = 8 // p = 1 q = 6 // m = 9 n = 3
a = 5 b = 8 c = 7 // p = 1 q = 4 // m = 6 n = 2
a = 6 b = 7 c = 4 // p = 1 q = 3 // m = 8 n = 5
a = 6 b = 8 c = 5 // p = 1 q = 3 // m = 7 n = 4
a = 6 b = 8 c = 7 // p = 1 q = 5 // m = 9 n = 4
a = 7 b = 8 c = 4 // p = 1 q = 3 // m = 9 n = 6
If I knew how to edit the former posts I would have done it. Maybe an admin can help.
a=3, b=4, c=6 // (1,2) // y=7x-5
a=3, b=4, c=6 // (1,5) // y=7x-2
I think it will depend on the definition of a “repeat”. These two solutions have the same equation but a different point and tangent line. If you allow unique solutions then these would count as two separate solutions. But you could limit the problem to insisting that each cubic equation is unique.
a=2, b=7, c=6 // (3, 9) // y=18x – 45