Directions: Use the digits 1 to 9, at most one time each, to create two equations: one where x has a positive value and one where x has a negative value.
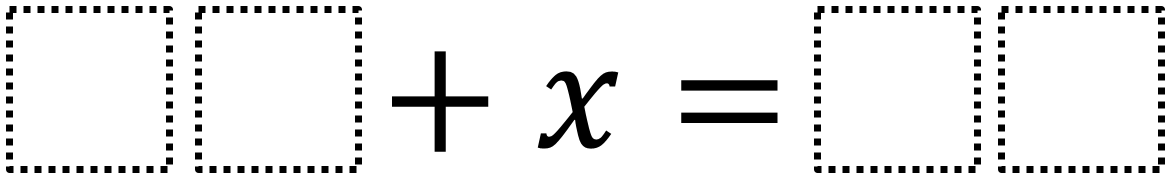
Hint
How does the value of the number being added to x affect the value of x?
How does the value of the sum affect the value of x?
How does the value of the sum affect the value of x?
Answer
There are many answers. To get a positive solution, the number being added to x should be less than the sum. To get a negative solution, the number being added to x should be greater than the sum.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Could you extend this by asking: ” Using the same digits, create an equation where x has a negative value. What do you notice?”
Sure. That’s a fine hint.
I love the critical thinking required in these questions, but this particular question isn’t a sixth grade Common Core standard. The standard, 6.EE.7, asks students to solve multiplication and addition equation with numbers that are all “nonnegative rational numbers”. Is there a way to align this question to the standard better while still preserving the DOK level? Students do not learn operations with negative numbers until the seventh grade.
X is positive:
1 x 3 + x = 2 x 6
3 + x = 12
x = 9
X is negative:
3 x 6 + x = 2 x 5
18 + x = 10
x = -8
Interesting that you interpreted the two boxes next to each other as multiplication. I was thinking they are two digit numbers.
Some positive solutions are:
13 + x = 25
24 + x = 35
Some negative solutions are:
25 + x = 13
35 + x = 24
Is it possible to do this and have x equal the same number in both equations? That’s originally what I thought I needed to do!
There are 756 unique solutions (times 2 because you could always swap the units digits of the first number and the sum) where x is positive.
There are equally as many where x is negative.
So in total, there are 756*756 = 571,536 possible pairs of equations where in one x is positive and in the other x is negative.
If you cannot repeat the digits for the two equations, then there are not 756*756 solutions, but “only” 22,680.