Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make each equation true.
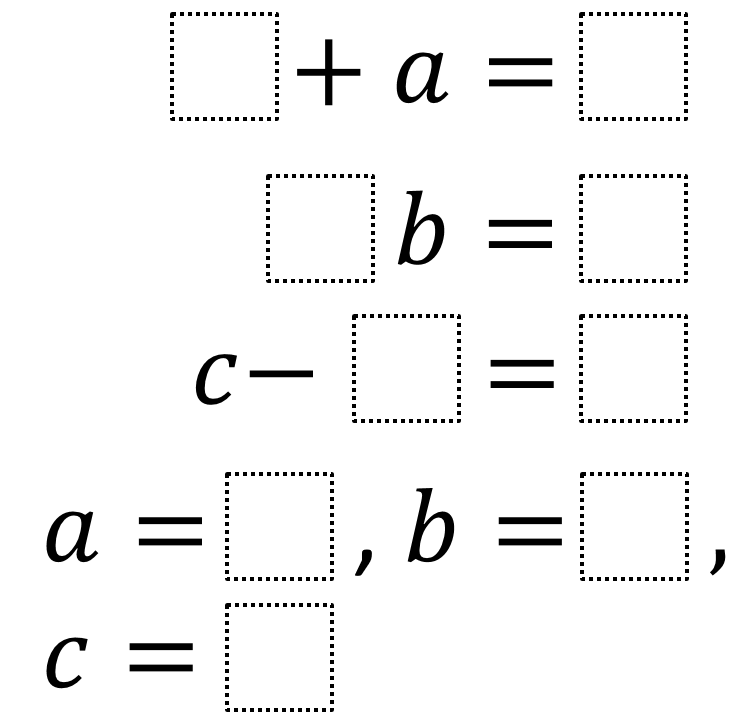
Hint
What is the largest possible value that the coefficient of b can be?
Answer
4 + a = 9
3 * b = 6
c – 7 = 1
a = 5, b = 2, c = 8
Number of Unique Solutions: 16
1: 1 + a = 8, 2b = 6, c – 4 = 5 with a = 7, b = 3, c = 9
2: 1 + a = 8, 2b = 6, c – 5 = 4 with a = 7, b = 3, c = 9
3: 1 + a = 8, 3b = 6, c – 4 = 5 with a = 7, b = 2, c = 9
4: 1 + a = 8, 3b = 6, c – 5 = 4 with a = 7, b = 2, c = 9
5: 4 + a = 9, 2b = 6, c – 1 = 7 with a = 5, b = 3, c = 8
6: 4 + a = 9, 2b = 6, c – 7 = 1 with a = 5, b = 3, c = 8
7: 4 + a = 9, 3b = 6, c – 1 = 7 with a = 5, b = 2, c = 8
8: 4 + a = 9, 3b = 6, c – 7 = 1 with a = 5, b = 2, c = 8
9: 5 + a = 9, 2b = 6, c – 1 = 7 with a = 4, b = 3, c = 8
10: 5 + a = 9, 2b = 6, c – 7 = 1 with a = 4, b = 3, c = 8
11: 5 + a = 9, 3b = 6, c – 1 = 7 with a = 4, b = 2, c = 8
12: 5 + a = 9, 3b = 6, c – 7 = 1 with a = 4, b = 2, c = 8
13: 7 + a = 8, 2b = 6, c – 4 = 5 with a = 1, b = 3, c = 9
14: 7 + a = 8, 2b = 6, c – 5 = 4 with a = 1, b = 3, c = 9
15: 7 + a = 8, 3b = 6, c – 4 = 5 with a = 1, b = 2, c = 9
16: 7 + a = 8, 3b = 6, c – 5 = 4 with a = 1, b = 2, c = 9
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



This answer does not seem to fit the problem (please let me know if I am missing something).
The answer I got was:
4 + a = 9
3 * b = 6
c – 7 = 1
a = 5, b = 2, c = 8
I am using this problem in PD tomorrow, so please let me know if there is an error in my thinking.
Thanks Barb. I’m not sure how that answer got switched into this problem. I can’t remember what answer I originally got. Your’s definitely works though. Probably others too.
Another student came up with
1+a=8
3b=6
c-4=5
a=7, b=2, c=9
The thought process in this question reminds me of Ken Ken Puzzles. These can be played on-line or you can receive an weekly email with printable puzzles. http://www.kenkenpuzzle.com/teachers/classroom
– I do not work for Ken Ken…just love them.
We, 6th-grade students, (Sivan and Diana) have also found another solution while using our teacher’s practice, it was:
1+a=8
3b=6
C-4=5
A=7
B=2
C=9
There are 8 unique solutions (times 2 because you could swap the two numbers in c – x = y to get another solution):
7 + a = 8; 3 * b = 6; c – 4 = 5; a = 1; b = 2; c = 9
7 + a = 8; 2 * b = 6; c – 4 = 5; a = 1; b = 3; c = 9
5 + a = 9; 3 * b = 6; c – 1 = 7; a = 4; b = 2; c = 8
5 + a = 9; 2 * b = 6; c – 1 = 7; a = 4; b = 3; c = 8
4 + a = 9; 3 * b = 6; c – 1 = 7; a = 5; b = 2; c = 8
4 + a = 9; 2 * b = 6; c – 1 = 7; a = 5; b = 3; c = 8
1 + a = 8; 3 * b = 6; c – 4 = 5; a = 7; b = 2; c = 9
1 + a = 8; 2 * b = 6; c – 4 = 5; a = 7; b = 3; c = 9
Which can be divided by 4 again, because 2 of them are the same as all the others, except that the addends in the first equation or the factors in the second equation are swapped, leaving us with only 2 unique solutions:
7 + a = 8; 3 * b = 6; c – 4 = 5; a = 1; b = 2; c = 9
5 + a = 9; 3 * b = 6; c – 1 = 7; a = 4; b = 2; c = 8