Open Middle®
Directions: Using the digits 0 to 9, at most one time each, place a digit in each box to make both of these equations true.
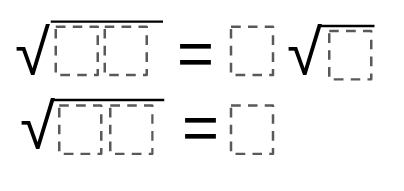
Hint
What are some two digit numbers that have a perfect square as a factor?
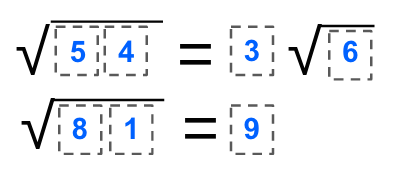
Answer
Multiple answers. Here is one possibility:
Number of Unique Solutions: 8
1: sqrt(16) = 2sqrt(4) and sqrt(9) = 3
2: sqrt(18) = 3sqrt(2) and sqrt(49) = 7
3: sqrt(54) = 3sqrt(6) and sqrt(81) = 9
4: sqrt(64) = 8sqrt(1) and sqrt(9) = 3
5: sqrt(72) = 3sqrt(8) and sqrt(16) = 4
6: sqrt(81) = 3sqrt(9) and sqrt(4) = 2
7: sqrt(09) = 3sqrt(1) and sqrt(64) = 8
8: sqrt(98) = 7sqrt(2) and sqrt(16) = 4
Source: Jonathan Newman
I think there are only three solutions. The one in the example and
Sqrt(18) = 3*Sqrt(2) ; Sqrt(49) = 7
Sqrt(98) = 7*Sqrt(2) ; Sqrt(16) = 4
Two additional possibilities:
09=3√1
√64=8
√64=8√1
√09=3
sq root of 64 equals 8 sq root 1
sq root of 49 equals 7