Directions: Using the digits 0 to 9 at most one time each, place a digit in each box so that each expression is simplified to a different odd number.
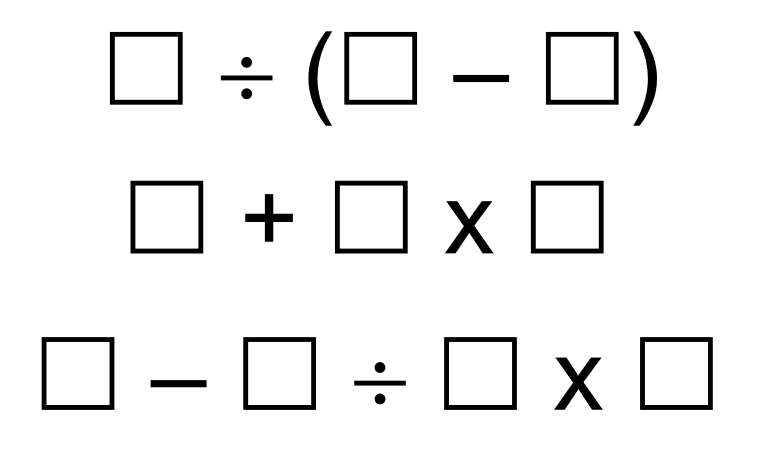
Hint
How do we know which digits are easier to place?
How can we tell which operations might affect getting a whole number result for our expression?
How can we tell which operations might affect getting a whole number result for our expression?
Answer
There are many different solutions to this problem.
5 ÷ (8 – 7) = 5
9 + 0 x 6 = 9
3 – 4 / 2 ÷ 1 = 1
Source: Molly Rawding
 Open Middle®
Open Middle® 


Is the intent to use each number only once in the ENTIRE set?
That is my understanding Katie.
i got 9 + 0 x 6 = 9
In confused
what do we do on this
hey I’m like really confused!!!
On the second set shouldn’t the answer be 54? I thought that when I was in school the math was done in order except for brackets. So the question should look like 9+(0*6)=9
I think you have to haeve an odd number and their are also many different answers for this.
HMMMMMMMMMMMMMMMMMMMMMMMMMM… Can we use decimals ¯\_(ツ)_/¯
I was forced to do this so I feel like this rn ¯\_(ツ)_/¯
so I feel like this rn ¯\_(ツ)_/¯
Too ez/easy
i am so confused
Can the answers be negative?
The possible solution given should end with multiplication in the equation, not division.
3 – 4 / 2 ÷ 1 = 1 should be 3 – 4 / 2 x 1 = 1
Not a big deal, just a typo.
My student and I got the following
7 / (6-5) =7
1 + 2 x 0 =1
9 – 8 / 4 x 3 =3
9 / (8-5) = 3
3 + 6 x 2 = 15 –> 3 + (6×2) = 15
7 – 4 / 1 x 0 = 7 —> 7-((4/1)x 0)) = 7
7 / ( 8 – 1 ) = 1
0 + 5 x 9 = 45
3 – 4 / 2 x 6 = 9
GOT A NEW ONE I THINK!!!
YES CORRECT
The third equation is incorrect because of order of operations. 3 – 4 / 2 x 6. The steps are:
3-4/2 x 6
3- 2 x 6
3 – 12
-9
I think you have to haeve an odd number and their are also many different answers for this.
There are 18,224 solutions (times 4, if you consider it a different solution if you swap the factors in the second expression or in the third expression)
5,827 of those have three positive results. 507 of the 5,827 results have three odd numbers between 0 and 10 as a result. The highest odd number that can be a result of on of those expression is 79 (=> second expression is 7 + 9 * 8), which makes the highest possible sum of all three expressions 6+79+5=90, for example: [6 / (4 – 3)] + [7 + 9 * 8] + [5 – 0 / 2 * 1]. The lowest possible sum (when all three results are positive) is 9, when the three expressions result in 1, 3 and 5, like in 1 / (6 – 5), 3 + 0 * 7, 9 – 8 / 4 * 2.
5,822 of the 5,827 solutions take advantage of the fact that:
1) odd number / (difference of any two numbers 1 apart) is odd (first expression) or that
2) odd number + 0 * any number is odd (second expression), or that
3) odd number – 0 / any number * any other number is odd (third expression).
So they’re very easy to create.
The other 5 solutions (unless again swapping factors counts as different solutions) are
6 / (2 – 0), 4 + 5 * 7, 8 – 9 / 3 * 1
6 / (2 – 0), 8 + 5 * 7, 4 – 9 / 3 * 1
9 / (3 – 0), 4 + 5 * 7, 8 – 6 / 2 * 1
9 / (3 – 0), 8 + 5 * 7, 4 – 6 / 2 * 1
9 / (3 – 0), 6 + 1 * 7, 5 – 8 / 4 * 2
which makes them my favorites (especially the last one, because the first four just swap the 6 and 9 or the 4 and 8, while the last one is very unique).
Don’t care + Didn’t ask
Boy you live in Washington LOL