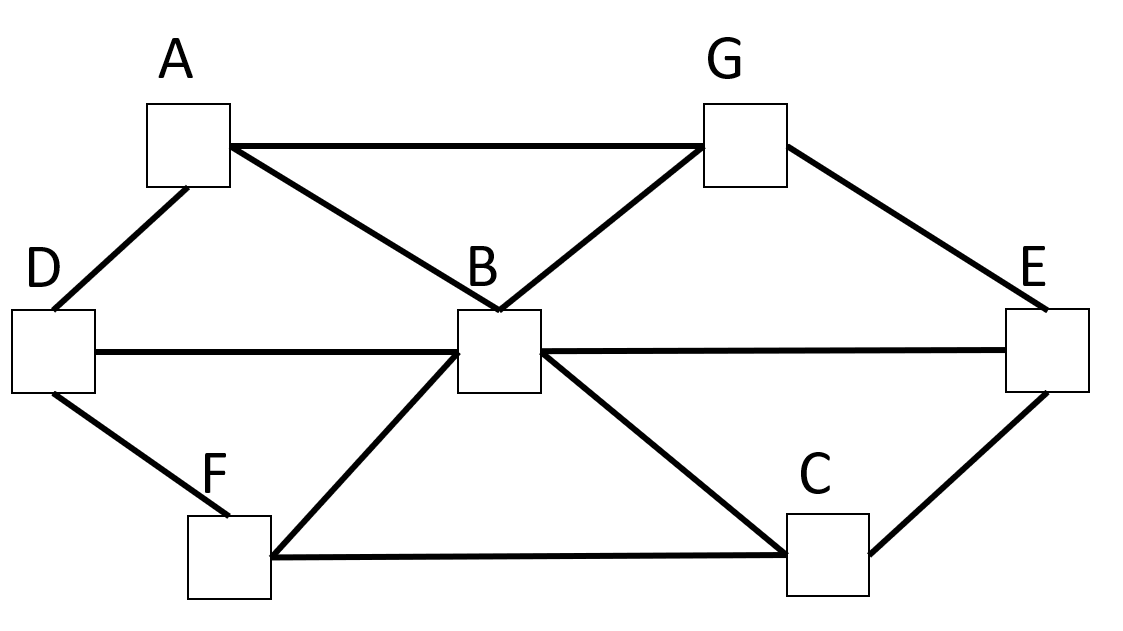
Directions: Using the digits 1 to 7, at most one time each, place a digit in each circle so that the sum of the numbers in 3 squares (the middle horizontal line or 2 diagonals) are same.
e.g A+B+C or D+B+E or F+B+G
Is there more than one solution?
Hint
Be strategic to think about the number in the center circle.
Answer
A possible answer
5 2
7 4 1
6 3
Source: Al Oz
 Open Middle®
Open Middle®



a=7 b=1 c=2
d=6 e=3
f=5 g=4
OMG I didn’t relize that!
A=2 B=7 C=5
D=3. E=4
F=1. G=6
or change the pairing to get similar solutions
52
741
63
hi c if ur reading dis
:]
also i got dat answer off d answer box thingy soz i CANNOT understand this
C d u understand this at all?
C ru there if UR then pleez rspond
? b
I don’t understand the directions. There are no circles in the image provided, but I guess the squares are the circles. But then the directions also mention squares. It says the sum of three squares should be the same – but the same as what? Each square contains only a single-digit-number, which are all different, so no 3 squares have the same “sum”.
Do you mean that the sums along the three lines ABC, FBG and DBE should be the same? In your example, the sum along ABC = the sum along DBE = the sum along FBG = 12.
In that case:
The possible sums of three different numbers from 1 to 7 are:
1+2+3=6
1+2+4=7
1+2+5=1+3+4=8
1+2+6=1+3+5=2+3+4=9
1+2+7=1+3+6=1+4+5=2+3+5=10
1+3+7=1+4+6=2+3+6=2+4+5=11
1+4+7=1+5+6=2+3+7=2+4+6=3+4+5=12
2+4+7=2+5+6=3+4+6=13
1+6+7=2+5+7=3+4+7=3+5+6=14
2+6+7=3+5+7=4+5+6=15
3+6+7=4+5+7=16
4+6+7=17
5+6+7=18
Only the sums 10, 12 and 14 have three sums where one of the numbers appears 3 times:
The sums 1+4+7=2+4+6=3+4+5=12 all have the number 4 and contain all natural numbers from 1 to 7.
The sums 1+2+7=1+3+6=1+4+5=10 all have the number 1 and contain all natural numbers from 1 to 7.
The sums 1+6+7=2+5+7=3+4+7=14 all have the number 7 and contain all natural numbers from 1 to 7.
So the only solutions other than the one provided by the author are
..2 4
3 1 6
..5 7
and
..1 2
3 7 4
..5 6
plus all the variants of these three solutions (8 each) where the endpoints of the lines ABC, BFG and/or DBE are swapped, for example
..6 2
3 7 4
..5 1
Forgot 1+5+7=13, but doesn’t provide another solution