Open Middle®
Directions: Using the digits 0 through 9 at most one time, place a digit in each box to make a true equation.
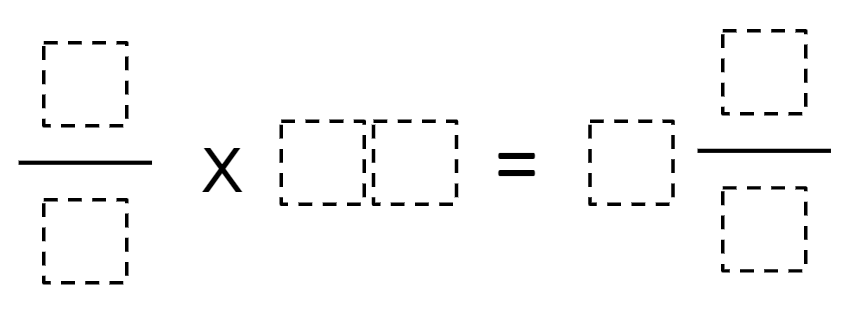
Hint
How can you make sure that your product is a mixed number?
Are there some two-digit numbers that don’t divide equally into groups?
How can you rename fractions so that you don’t use the same digit more than once?
Are there some two-digit numbers that don’t divide equally into groups?
How can you rename fractions so that you don’t use the same digit more than once?
Answer
There are multiple solutions. One is 2/4 x 17 = 8 3/6.
Source: Ellen Metzger
Wow. This took me a while… 8 tries. But very satisfying.
2/4 x 15 = 7 3/6
3/4 x 09 = 6 3/4
1/3 x 08 = 2 6/9
If zero cannot be used to start the two-digit number:
1/4 x 23 = 5 6/8
1/8 *60=7 2/4
5/6 x10= 8 3/9
1/8 x 76 = 9 2/4
2/8 x 37=9 1/4
If zero can be used to start the two-digit number:
5/6 x 09 = 7 4/8
5/6 x 09 = 7 1/2
2/4 x 05= 7 and 3/6
3/8 x 06 = 2 1/4
4/3 x 07 = 9 2/6
1/2 x 07 = 3 4/8
5/4 x 06=7 1/2
3/4 x 07 = 5 2/8
6/8 x 07 = 5 1/4
If zero cannot be used to start the two-digit number (because then it wouldn’t be a two-digit number anymore), as the whole part of the mixed number (because then it would’t be a mixed number anymore) or as the numerator of the fractional part of the mixed number (because then again it wouldn’t be a mixed number anymore) and if the fractional part of the whole number has to be a proper fraction, then there are 23 solutions (164 if the fractional part of the mixed number can be an improper fraction) ranging from 5.3333… to 9.666…:
1/9 * 48 = 5 2/6 = 5.3333
3/9 * 17 = 5 4/6 = 5.6667
1/4 * 23 = 5 6/8 = 5.75
4/9 * 15 = 6 2/3 = 6.6667
1/8 * 60 = 7 2/4 = 7.5
2/4 * 15 = 7 3/6 = 7.5
3/6 * 15 = 7 2/4 = 7.5
3/6 * 15 = 7 4/8 = 7.5
4/8 * 15 = 7 3/6 = 7.5
5/8 * 12 = 7 3/6 = 7.5
6/8 * 10 = 7 2/4 = 7.5
1/8 * 62 = 7 3/4 = 7.75
1/6 * 50 = 8 3/9 = 8.3333
1/9 * 75 = 8 2/6 = 8.3333
5/6 * 10 = 8 3/9 = 8.3333
2/4 * 17 = 8 3/6 = 8.5
3/6 * 17 = 8 2/4 = 8.5
1/4 * 37 = 9 2/8 = 9.25
2/8 * 37 = 9 1/4 = 9.25
1/6 * 57 = 9 2/4 = 9.5
1/6 * 57 = 9 4/8 = 9.5
1/8 * 76 = 9 2/4 = 9.5
1/6 * 58 = 9 2/3 = 9.6667
Out of these, the following 3 are the only ones that contain only irreducible fractions, making them my favorite solutions:
4/9 * 15 = 6 2/3
1/8 * 62 = 7 3/4
1/6 * 58 = 9 2/3
If you allow 0 to start the two-digit number and to be the whole part or the numerator of the fractional part of the mixed number and you allow the fractional part of the mixed number to be an improper fraction, then there are 548 solutions ranging from 1.3333… to 16.
Unfortunately, it seems something prevents me from posting the additional 525 solutions here (even if I only try to post ~100 solutions at a time, my comments don’t show up). So here are just a few example solutions with all restrictions lifted:
1/2*07=3 4/8 (0 starts the two-digit number)
1/3*24=8 0/5 (0 as the numerator of the fractional part of the mixed number)
1/8*36=0 9/2 (0 as the whole part of the mixed number, +improper fraction)
1/3*25=7 8/6 (improper fraction as the fractional part of the mixed number)
Whyyyyyyyyyyyyyyyyyyyyy One is 2/4 x 17 = 8 3/6.
Rudolf you are very smart thanks for the answer
Ryan what is the answer