Open Middle®
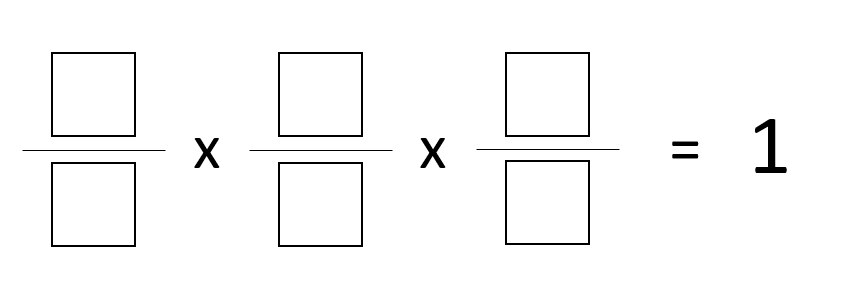
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to make a true statement.
Hint
Could some of the fractions have a value greater than 1?
Answer
3/4 * 6/9 * 2/1 = 1
Source: Owen Kaplinsky, Answer by Joseph Nguyen
4/1 x 1/2 x 1/2
4/1 x 1/2 x 1/2 = 1
4/1 x 1/2 x 1/2=1
i got 3/4 x 6/9 x 2/1 = 1
3/4 x 6/9 x 2/1 = 1
One of my students did: 6/9 x 4/8 x 3/1
Excellent for factors and multiples lessons.
I did 3/4x 6/4×2/1=1
One of my students found 1/6×9/3×8/4=1
3/4 * 6/5 * 10/9
9/3 * 1/6 * 4/2 = 1
9/3 * 1/6 8 8/4 = 1
The unique solutions are:
1/2 * 4/3 * 9/6
1/3 * 8/6 * 9/4
You can always swap the numerators or the denominators (x6) or the whole fractions (x6) around or take the reciprocal of all three fractions (x2) to get 6*6*2=72 times as many solutions (so, in total, 144 solutions).
In other words: Use any permutation of the numbers 1,4,9 for the numerator and 2,3,6 for the denominator (or vice versa) or use any permutation of the numbers 1,8,9 for the numerator and 3,4,6 for the denominator (or vice versa).
Unfortunately I can’t post the whole list due to some comment/text limit on this website.
The reason these are the (only) solutions is because the only ways to get the same number as a product of three numbers between 1 and 9 in 2 ways (once for the denominator and once for the numerator) such that each of the 6 numbers is different are: 1*4*9 = 2*3*6 = 36 and 1*8*9 = 3*4*6 = 72.
This problem (created in December 2019) is the same as another one called “Fraction Multiplication Equal to 1” posted in May 2018.
Here’s the link: https://www.openmiddle.com/fraction-multiplication-equal-to-1/
1/1 * 1/1 * 1/1