Open Middle®
Directions: Using the digits 1 to 9, at most one time each, create an equation where x has a positive (or negative) value.
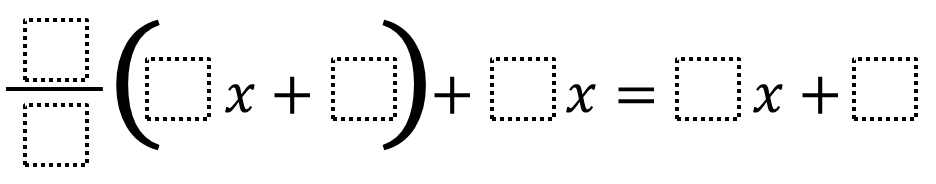
Hint
What makes a solution positive (or negative)?
Where do you want to put the larger (or smaller) numbers?
Where do you want to put the larger (or smaller) numbers?
Answer
There are many solutions that would work.
Example that would give a positive solution:
(1/2)(4x + 8) + 6x = 9x + 3 … here, x = 1
Example that would give a negative solutions
(1/3)(6x + 9) + 2x = 5x + 7 … here, x = -4
Another constraint or extension you could add is change the directions to say: “Use the digits 1 to 9, at most one time each, to create an equation where x has a positive (or negative) integer value.”
Source: Daniel Luevanos
(1/3)(6x+9)+2x=5x+7
x=-4
(1/2)(4x+8)+6x=9x+3
x=1
3/6(2x+4)+7x=6x+5
x= 1.5
2/6(4x+8)+7x=3x+9
x=1.2
1/3(4+8)+2x=2x+8
x=4
1/2(5x+6)+3x=4x+9
X=4
1/2(-9x(4)=8x(2)
(1/2)(4x + 8) + 6x = 9x + 3
which is 1
(1/2)(4x + 8) + 6x =9x + 3
which is 1
5/3 (6x+3+1x=4x+3
x=-0.28
3/4(8x+7)+3x=11x+2
1/2(4x-2)+3x=-2x+4
x=5
1/2x(2x-1)+4x=-6x+2
x=no solution
2/3x-1/6=1/2x+5/6
x=6
(1/2)(4x+8)+6x=9x+3
x=1
2/1(4x+6)+7x=5x+8
(1/2)(4x+9)+6x= 7x+2
1/2(5x+6)+3x=4x+9 X=4
1/5 (3x + 2) + 4x = 6x + 8
X=6
1/5 (3x + 2) + 4x = 6x + 8
X=6
3/4m−2(m−1)= 1/4m+5
m=-2
1/6(2x+3)+7x=-12+10
x=3
1/6(1x+9)+2x=4x+6
x=5
1/2 ( 4x + 8 ) -2 = 4x + 3
x = -1/2
1/2(4x+6)+5x=7x+3 which means x = 0
3/6(3x+5)+2x=5x+6
which means x=-7/3