Directions: Using the digits 1 to 20, at most one time each, fill in the boxes to create equivalent expressions.
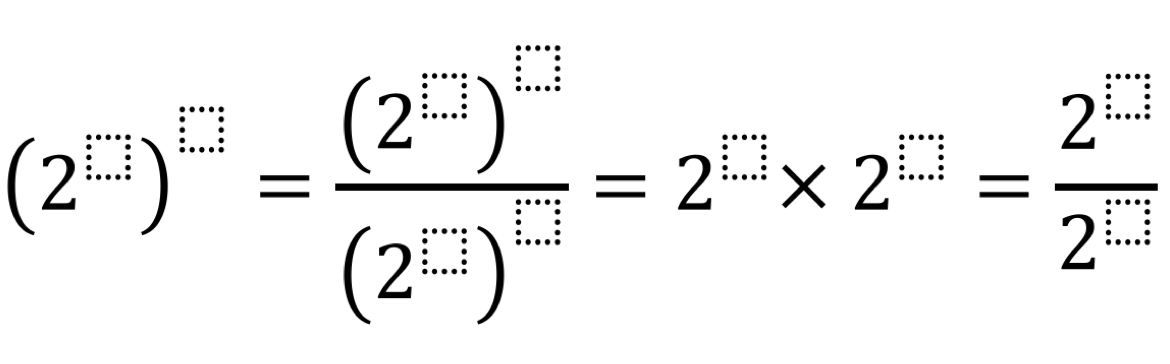
Hint
What types of numbers are easy to arrange into products?
Answer
There are many possible solutions. For example,
(2^3)^4 = ((2^5)^12)/((2^6)^8) = 2^10 x 2^2 = (2^19)/(2^7)
(2^2)^5 = ((2^6)^11)/((2^7)^8) = 2^1 x 2^9 = (2^20)/(2^10)
More solutions are given in the comments
Source: Shaun Errichiello
 Open Middle®
Open Middle®



This problem was fantastic! My awesomely skilled sixth graders found seven more solutions to this problem! I wonder if we found them all? Thank you!
Good on them! But not sure they did find them all Mr Breadstick (see Julie’s comment below)
I see that some students have found more solutions. I thought I might share a solution found by one of my 8th graders.
(2^2)^5 = (2^6)^11/(2^7)^8 = 2^3 x 2^7 = 2^20/2^10
We found a mistake ( that is after I double checked. ugh!) change 2^3 x 2^7 to 2^1 x 2^9
Well done to your 8th grader Holly. I’ve added their solution to the answers!
I think I found a ton that all equal 32. First I rewrote it:
(2^a)^b = (2^c)/(2^d) = 2^g * 2^h = 2^j / 2^k
Then {a,b,c,d,e,f,g,h,j,k} can be
1,5,4,17,7,9,2,3,11,6
1,5,4,17,7,9,2,3,13,8
1,5,4,17,7,9,2,3,15,10
1,5,4,17,7,9,2,3,16,11
1,5,4,17,7,9,2,3,18,13
1,5,4,17,7,9,2,3,19,14
1,5,4,17,7,9,2,3,20,15
1,5,7,11,4,18,2,3,15,10
1,5,7,11,4,18,2,3,17,12
1,5,7,11,4,18,2,3,19,14
1,5,7,11,4,18,2,3,20,15
or any permutation of any of these that switches the numbers in the a,b and/or c,d and/or e,f and/or g,h pairs.
I suspect there are a lot of other solutions too!
there are 102400 possible combonations
i think
I got a different answer than the one provided. I got:
(2^2)^3 = (2^15)^6/(2^7)^12= 2^1 x 2^5 = 2^10/2^4
Did anyone else get this answer? Is this correct?
There are lots of possible solutions Amy. Yours is correct – well done!
Any chance we could change the word “digits” to numbers since 11-20 are not digits?
one solution I have is:
(2^2)^9 = {(2^6)^5}/{(2^3)^4} = (2^11) x (2^7) = (2^19)/(2^1)
I have this same problem, but the directions say I can only use digits 0-9. Can anyone come up with a solution?
(2^2)^5 = {(2^6)^11}/{(2^7)^8} = 2^1 x 2^9 = 2^20/2^10
I just spent more time than I should have finding solutions where all of the exponents simplify to 5, 6, 7, all the way to 18. I know I didn’t find all of the solutions, but I think those are all of the possible exponents. You can’t simplify to anything less than 5 because you would have to use two 1s, and you can’t simplify to 19 for the same reason. Thanks for a great problem
a little feedback – “using the digits 1-20” is not strictly correct terminology, otherwise a very cool task