Open Middle®
Directions: What is the least number of geometric markings needed to demonstrate that a quadrilateral is a square?
Hint
What markings would make a quadrilateral a square?
What are the properties of a square that make it unique to the other quadrilaterals?
Answer
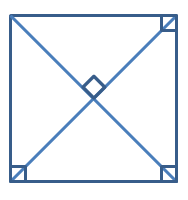
Four markings are needed because the three right angles at the vertices prove that the quadrilateral is a rectangle and the right angle at the intersection of the diagonals prove that it is a rhombus. The quadrilateral is a rectangle and a rhombus, so then the quadrilateral must be a square.
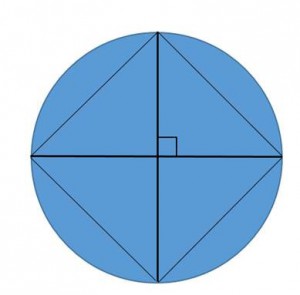
Here is what Amy Gross came up with at a CMC-South presentation.
She said, “If you start with a circle…” and we were all blown away.
The diameters are perpendicular. The adjacent endpoints of the diameter are connected with segments to form a quadrilateral, which can be proved to be a square. The problem that we are having is figuring out how many markings this would count as. How many would you count?
Source: A collaborative effort of Jose De La Torre and Nanette Johnson answer by Ricardo Navarro with help from Robert Kaplinsky
