Open Middle®
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to find the largest/smallest possible sum of the three terms in this finite geometric series.
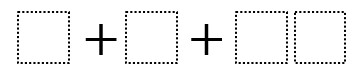
Hint
How do you generate the terms of a geometric series?
Answer
The largest possible sum we found was 73 (1 + 8 + 64). The smallest possible sum we found was 21 (3 + 6 + 12).
Source: Dana Harrington
The largest we got was 6+7+98 = 111
The smallest we got was 3 + 4 + 12 = 19
Am I doing something wrong or am I correct here?
Hi Matt,
If the prompt didn’t specify that it was a geometric series, then I think you would be correct! I think your class successfully found the largest and smallest sum for this format in general without the constraint of it having to be a geometric series.
To make it a geometric series, there needs to be a common ratio between each consecutive term. For example, 1 + 8 + 64 is a geometric series because you multiply each term by 8 to get the next term.
thank you!