Open Middle®
Directions: Using the digits 0 to 9, at most one time each, place a digit in each box to make a derivative as close to 100 as possible.
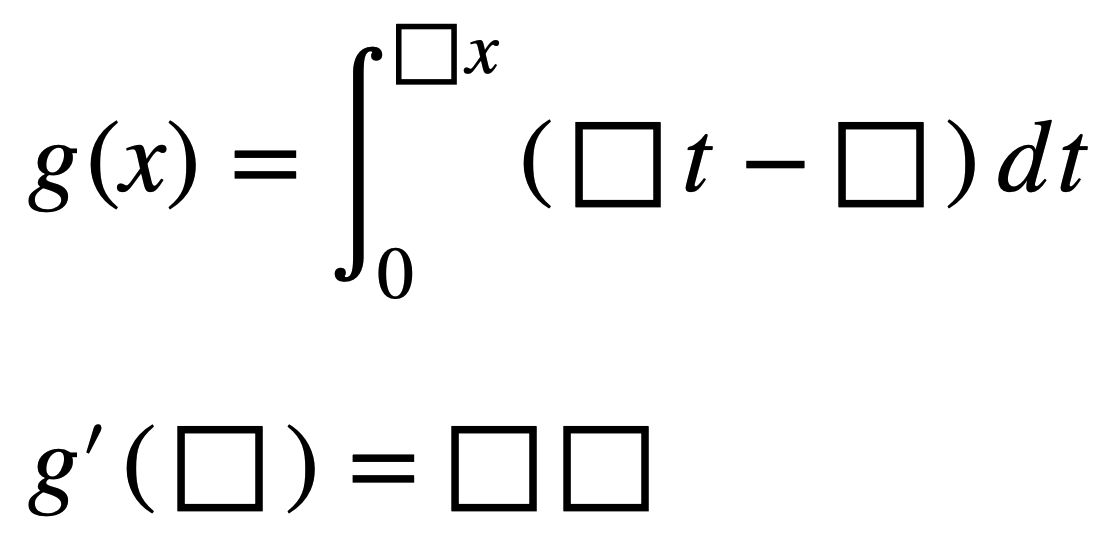
Hint
Try replacing the blanks – not the result of g'(_) – with a, b, c, d. Then compute the derivative algebraically.
g(x) = the integral of (at-b) with respect to t from 0 to Dx
g'(c) = _ _
g(x) = the integral of (at-b) with respect to t from 0 to Dx
g'(c) = _ _
Answer
g(x) = the integral of (at-b) with respect to t from 0 to Dx
g'(c) = _ _
g'(c) = _ _
(a, b, c, d, val) = ( 1 , 0 , 2 , 7 , 98 )
(a, b, c, d, val) = ( 2 , 0 , 1 , 7 , 98 )
If the minus sign in the integrand is changed to a plus sign, the solutions are
(a, b, c, d, val) = ( 1 , 0 , 2 , 7 , 98 )
(a, b, c, d, val) = ( 2 , 0 , 1 , 7 , 98 )
(a, b, c, d, val) = ( 4 , 1 , 6 , 2 , 98 )
(a, b, c, d, val) = ( 6 , 1 , 4 , 2 , 98 )
Source: Stephen Spinelli
Good task! Isn’t (a, b, c, d, val) = (1, 3, 7, 2, 56) also a solution?