Open Middle®
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to make two fractions that have a quotient that is as close to 4/11 as possible.
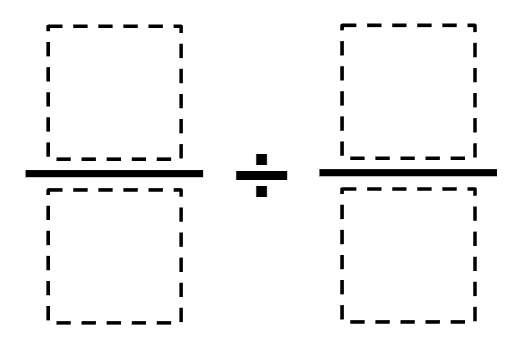
Hint
How can we figure out how close a fraction is to 4/11?
How can we tell which of two fractions is closer to 4/11?
How can we tell which of two fractions is closer to 4/11?
Answer
The optimal answer is 5/7 ÷ 2/1 (or equivalents like 5/7 ÷ 4/2 or 5/7 ÷ 6/3 or 5/7 ÷ 8/4). Carlie found another set of answers is including 1/2 ÷ 7/5 (or equivalents like 2/4 ÷ 7/5 or 3/6 ÷ 7/5 or 4/8 ÷ 7/5)
Source: Robert Kaplinsky
5/7 divided by 1/2 is 10/7. Did you mean 7/5 divided by 2/1?
Yep. You were right and I just made the change. Thanks!
Hey There. I was a bit confused as to why the listed answer was optimal like Hannah above.
One of my students just came up with (4/5) divided by (2/1)=4/10 which is pretty darn close, and definitely closer than 10/7.
Thanks for providing these great problem solving resources!
Yeah, I copied this over from a multiplication version and forgot to invert the fractions. Sorry!
Absolutely no need to apologize! I am very appreciative of all your time and hard work to share all your amazing ideas and materials with us! My students are too as they all love and request more of these types of problems whenever we happen to work on any!
I think it’s 1/2 ÷ 5/7 because that is approximately 0.357, while 4/11 is 0.36363636…
oops… I mean 1/2 divided gy 7/5
Yep, that’s an equivalent answer to the one listed. Thanks. I’ll add it.
4/6 divided by 2/1 equals 1/3
The 16 divisions
1/2 ÷ 7/5
1/7 ÷ 2/5
2/4 ÷ 7/5
2/7 ÷ 4/5
3/6 ÷ 7/5
3/7 ÷ 6/5
4/7 ÷ 8/5
4/8 ÷ 7/5
5/2 ÷ 7/1
5/4 ÷ 7/2
5/6 ÷ 7/3
5/7 ÷ 2/1
5/7 ÷ 4/2
5/7 ÷ 6/3
5/7 ÷ 8/4
5/8 ÷ 7/4
are all equal to = 5/14 = 4/11 + 0.0064935064935…., but they really are all the same, because
a/b ÷ c/d = a/c ÷ b/d = d/b ÷ c/a = d/c ÷ b/a (multiplying the number of solutions by 4) and
1/2 = 2/4 = 3/6 = 4/8 (multiplying again by 4).