Fraction Equivalence

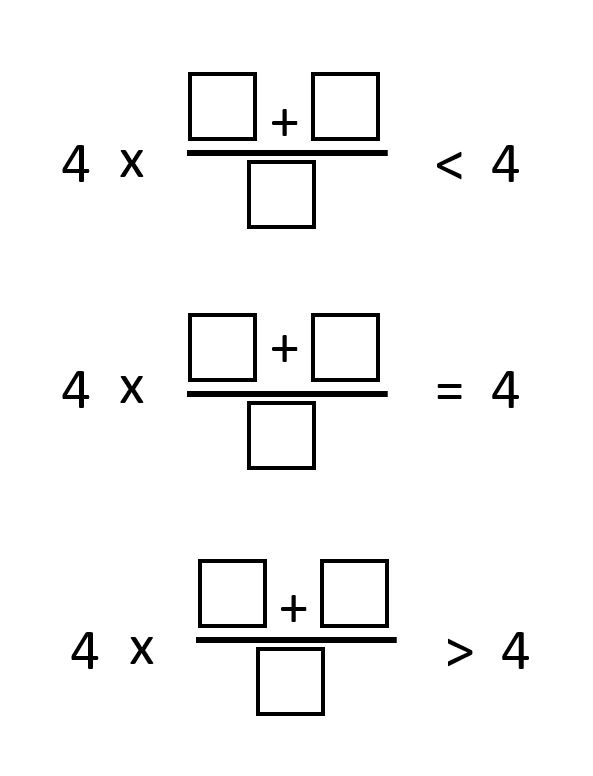
Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to create a fraction that correctly completes each statement.

Hint

What is the result of multiplying a whole number by a proper fraction?
What is the result of multiplying a whole number by an improper fraction?

Answer

Multiple answers:

ex. (1+3)/9 < 4, (6+2)/8 = 4, (5+7)/4 > 4

Source: Ian Kerr

Tags 5.NF.5 DOK 2: Skill / Concept Ian Kerr

Check Also

Add Fractions with Decimal Sums

Directions: Using the digits 1 to 9 at most one time each, place a digit …

2 comments

Rudolf Österreicher
July 10, 2023 at 8:30 pm

317 solutions:
4 * (1 + 2)/4 4.
4 * (1 + 2)/4 4.
4 * (1 + 2)/4 4.
4 * (1 + 2)/4 4.
4 * (1 + 2)/4 4.
4 * (1 + 2)/4 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/5 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/6 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/7 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/8 4.
4 * (1 + 2)/9 4.
4 * (1 + 2)/9 4.
4 * (1 + 2)/9 4.
4 * (1 + 2)/9 4.
4 * (1 + 2)/9 4.
4 * (1 + 2)/9 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/5 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/6 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/7 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/8 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 3)/9 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/6 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/7 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/8 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 4)/9 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/7 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/8 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 5)/9 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/8 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 6)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (1 + 7)/9 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/6 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/7 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/8 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 3)/9 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/7 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/8 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 4)/9 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/8 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 5)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (2 + 6)/9 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/8 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 4)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.
4 * (3 + 5)/9 4.

Reply
- Rudolf Österreicher
  July 10, 2023 at 9:31 pm
  
  Unfortunately, the comment got messed up when posted and I can’t edit it and it won’t let me post the list again, even formatted differently.
  
  But it’s really easy to create solutions. Start wie the middle one. The fraction has to have a value of 1, so the numerator and denominator have to be equal. So the middle fraction can be (1+2)/3, (1+3)/4, (1+4)/5, (1+5)/6, (1+6)/7, (1+7)/8, (1+8)/9, (2+3)/5, (2+4)/6, (2+5)/7, (2+6)/8, (2+7)/9, (3+4)/7, (3+5)/8, (3+6)/9 or (4+5)/9 (or swapping the addends in the numerator). Then use the remaining 6 numbers such that in the first fraction, the sum in the numerator is less then the denominator and in the third fraction the sum in the numerator is greater than the denominator.
  
  Reply

Open Middle®