Open Middle®
Directions: Using the digits 1 to 9 at most one time each, place a digit in each box to make a correct equation.
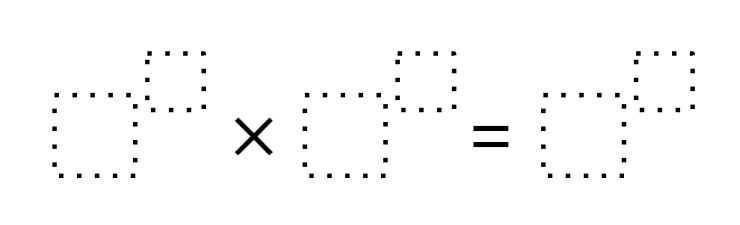
Hint
How might three powers with different bases satisfy this equation?
Answer
Some of the possible answers: 2^7 x 4^1 = 8^3, 2^9 x 4^3 = 8^5, 1^7 x 3^4 = 9^2, 1^4 x 2^9 = 8^3. Clearly other powers of 1 work too.
Source: Stephen Cox
60 solutions (120 if you swap factors). 48 of them contain powers of one. Here are the other 12:
2^1 * 4^7 = 8^5
2^1 * 8^3 = 4^5
2^3 * 4^6 = 8^5
2^3 * 4^9 = 8^7
2^3 * 8^5 = 4^9
2^5 * 8^3 = 4^7
2^7 * 4^1 = 8^3
2^7 * 8^1 = 4^5
2^9 * 4^3 = 8^5
2^9 * 4^6 = 8^7
2^9 * 8^1 = 4^6
4^3 * 8^1 = 2^9
And here the 48 solutions with powers of 1:
1^2 * 3^8 = 9^4
1^2 * 4^9 = 8^6
1^2 * 8^6 = 4^9
1^2 * 9^4 = 3^8
1^3 * 4^9 = 8^6
1^3 * 8^6 = 4^9
1^4 * 2^9 = 8^3
1^4 * 8^3 = 2^9
1^5 * 2^6 = 4^3
1^5 * 2^9 = 8^3
1^5 * 3^4 = 9^2
1^5 * 3^8 = 9^4
1^5 * 4^3 = 2^6
1^5 * 4^3 = 8^2
1^5 * 4^9 = 8^6
1^5 * 8^2 = 4^3
1^5 * 8^3 = 2^9
1^5 * 8^6 = 4^9
1^5 * 9^2 = 3^4
1^5 * 9^4 = 3^8
1^6 * 2^9 = 8^3
1^6 * 3^4 = 9^2
1^6 * 3^8 = 9^4
1^6 * 4^3 = 8^2
1^6 * 8^2 = 4^3
1^6 * 8^3 = 2^9
1^6 * 9^2 = 3^4
1^6 * 9^4 = 3^8
1^7 * 2^6 = 4^3
1^7 * 2^9 = 8^3
1^7 * 3^4 = 9^2
1^7 * 3^8 = 9^4
1^7 * 4^3 = 2^6
1^7 * 4^3 = 8^2
1^7 * 4^9 = 8^6
1^7 * 8^2 = 4^3
1^7 * 8^3 = 2^9
1^7 * 8^6 = 4^9
1^7 * 9^2 = 3^4
1^7 * 9^4 = 3^8
1^8 * 2^6 = 4^3
1^8 * 3^4 = 9^2
1^8 * 4^3 = 2^6
1^8 * 9^2 = 3^4
1^9 * 2^6 = 4^3
1^9 * 4^3 = 2^6
1^9 * 4^3 = 8^2
1^9 * 8^2 = 4^3
bruh I don unde stand