Directions: Using the digits 1 to 9, at most one time each, fill in the boxes to make a result that has the greatest value possible.
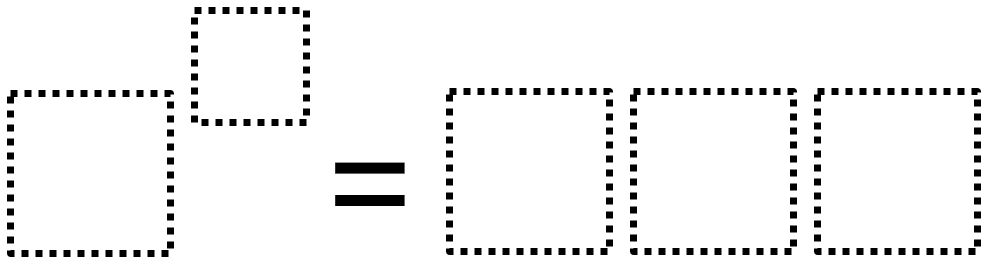
Hint
How does changing the base affect the value?
How does changing the exponent affect the value?
How does changing the exponent affect the value?
Answer
Initially, some students may think that the answer is 8^9. This breaks the structure of the problem, as the result has to be 3-digits.
The largest possible 3-digit result is 729 from 3^6 = 729.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



The given answer is incorrect. Although 9^3 = 729, the directions say to use each digit “at most one time each.” This answer repeats the digit 9.
You’re totally right, Patrick. I’ll change it to just the single answer.
I have always loved these open middle problems! But I do wonder if there’s room for some discussion on why the right answer is the right answer, or a potential thought process to go through.
Here is what my thought process was:
Let me try a base of nine because that’s a nice big number. But the highest exponent I could use without getting a four digit answer is 3, and that only gives me 729. (Which also has two 9’s which isn’t allowed. But knowing exponent rules, nine to the third power is the same as three to the sixth power. so my best Answer so far is 3^6=729 since none of those digits, repeat.)
I wonder if there’s another answer that would give something larger than 729. No single digit to the third power will get me a larger answer then nine to the third power. so maybe a single digit to the fourth power is the answer. But eight to the fourth power, seven to the fourth power, and six to the fourth power are all four digits. Five to the fourth power is only three digits! But it’s not as large as 729. …
I carried on that logic all the way through, looking at the fifth power, and sixth power.