Directions: Find values for a and b that will make the expressions equivalent, assuming that a does not equal b.
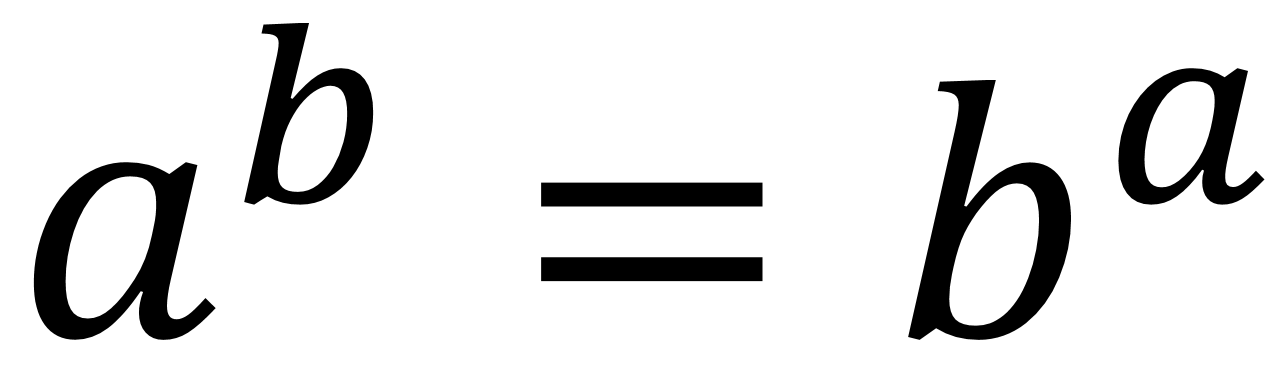
Hint
How does each base’s factors affect the equivalence?
Answer
There are two possible answers. One is when a and b are 2 and 4, giving 2^4 = 4^2. The other was found by Shashi and is when a and b are -2 and -4, giving (-2)^(-4) = (-4)^(-2).
Source: Owen Kaplinsky
 Open Middle®
Open Middle®



-2, -4
Oh! I didn’t think of that!
I think have more answer like ;a=1,b=1 this is one answer:a=-1,b=-1
Unfortunately, this won’t work because it says that a cannot equal b.
Thanks for telling me this!
Nice one! I’ll add it to the answers.
a=1/2
b=4
a=1/4
b=2
Thank you sooooo much
a^b = b^a
Substitute b = ua: a^(ua) = (ua)^a
=> (a^u)^a = (ua)^a
=> ((a^u)^a)^(1/a) = ((ua)^a)^(1/a)
=> a^u = ua
=> (a^u)/a = u
=> a^(u-1) = u
=> (a^(u-1))^(1/(u-1)) = u^(1/(u-1))
=> a = u^(1/(u-1))
=> b = u * a = u * u^(1/(u-1))
=> b = u^(1/(u-1) + 1) = u^(1/(u-1) + (u-1)/(u-1)) = u^(u/(u+1))
With the expressions a = u^(1/(u-1)) and b = u^(u/(u+1)), we can now get every possible solution by plugging in any real number u..
If we plug in u = 4 for example, then we get a = cuberoot(4) and b = 4*cuberoot(4).
If we plug in u = 2 or 1/2, we get a = 2 and b = 4 (or vice versa)
Another solution is a = sqrt(3) and b = 3*sqrt(3)
There are infinitely many rational solutions like a = 27/8, b = 9/4 (or vice versa), but only one solution in the natural numbers: a = 2 and b = 4 (or vice versa), because for all natural numbers n>0 and a>=3, a^(a+n) > (a+n)^a, so a (and, by symmetry, b) can’t be greater than 2.
For more info, Wikipedia has a good article titled “Equation x^y = y^x”.