Open Middle®
Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to create two equivalent expressions.
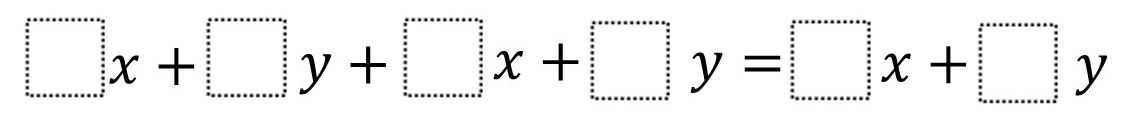
Hint
What terms can you combine on the left side?
Answer
Here are some possibilities:
1x+2y+5x+7y=6x+9y
2x+3y+4x+5y=6x+8y
2x+4y+1x+5y=3x+9y
Source: James Cresswell
There are 50 unique solutions:
1x + 2y + 3x + 5y = 4x + 7y
1x + 2y + 3x + 6y = 4x + 8y
1x + 2y + 3x + 7y = 4x + 9y
1x + 2y + 4x + 6y = 5x + 8y
1x + 2y + 4x + 7y = 5x + 9y
1x + 2y + 5x + 7y = 6x + 9y
1x + 3y + 4x + 6y = 5x + 9y
1x + 3y + 5x + 4y = 6x + 7y
1x + 3y + 6x + 5y = 7x + 8y
1x + 3y + 7x + 6y = 8x + 9y
1x + 4y + 2x + 5y = 3x + 9y
1x + 4y + 6x + 5y = 7x + 9y
1x + 4y + 7x + 5y = 8x + 9y
2x + 1y + 3x + 6y = 5x + 7y
2x + 1y + 3x + 7y = 5x + 8y
2x + 1y + 3x + 8y = 5x + 9y
2x + 1y + 4x + 7y = 6x + 8y
2x + 1y + 4x + 8y = 6x + 9y
2x + 1y + 5x + 8y = 7x + 9y
2x + 3y + 4x + 5y = 6x + 8y
2x + 3y + 5x + 6y = 7x + 9y
2x + 4y + 6x + 5y = 8x + 9y
3x + 1y + 4x + 8y = 7x + 9y
3x + 2y + 4x + 6y = 7x + 8y
3x + 2y + 5x + 7y = 8x + 9y
Plus another 25 where all the x- and y-coefficients are swapped.
Of course you can always swap around the two x-terms and/or the two y-terms on the left, to get four times as many solutions, so 200.