Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to create two equivalent expressions.
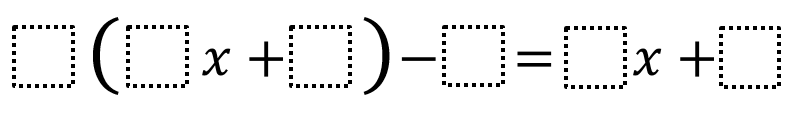
Hint
How does subtracting a number affect the left side of the equation?
Answer
Number of Unique Solutions: 26
1: 2(3x + 4) – 1 = 6x + 7
2: 2(3x + 4) – 7 = 6x + 1
3: 2(3x + 5) – 1 = 6x + 9
4: 2(3x + 5) – 9 = 6x + 1
5: 2(3x + 7) – 5 = 6x + 9
6: 2(3x + 7) – 9 = 6x + 5
7: 2(3x + 8) – 7 = 6x + 9
8: 2(3x + 8) – 9 = 6x + 7
9: 2(4x + 3) – 1 = 8x + 5
10: 2(4x + 3) – 5 = 8x + 1
11: 2(4x + 5) – 1 = 8x + 9
12: 2(4x + 5) – 3 = 8x + 7
13: 2(4x + 5) – 7 = 8x + 3
14: 2(4x + 5) – 9 = 8x + 1
15: 2(4x + 6) – 3 = 8x + 9
16: 2(4x + 6) – 5 = 8x + 7
17: 2(4x + 6) – 7 = 8x + 5
18: 2(4x + 6) – 9 = 8x + 3
19: 2(4x + 7) – 5 = 8x + 9
20: 2(4x + 7) – 9 = 8x + 5
21: 3(2x + 4) – 5 = 6x + 7
22: 3(2x + 4) – 7 = 6x + 5
23: 3(2x + 5) – 7 = 6x + 8
24: 3(2x + 5) – 8 = 6x + 7
25: 4(2x + 3) – 5 = 8x + 7
26: 4(2x + 3) – 7 = 8x + 5
1: 2(3x + 4) – 1 = 6x + 7
2: 2(3x + 4) – 7 = 6x + 1
3: 2(3x + 5) – 1 = 6x + 9
4: 2(3x + 5) – 9 = 6x + 1
5: 2(3x + 7) – 5 = 6x + 9
6: 2(3x + 7) – 9 = 6x + 5
7: 2(3x + 8) – 7 = 6x + 9
8: 2(3x + 8) – 9 = 6x + 7
9: 2(4x + 3) – 1 = 8x + 5
10: 2(4x + 3) – 5 = 8x + 1
11: 2(4x + 5) – 1 = 8x + 9
12: 2(4x + 5) – 3 = 8x + 7
13: 2(4x + 5) – 7 = 8x + 3
14: 2(4x + 5) – 9 = 8x + 1
15: 2(4x + 6) – 3 = 8x + 9
16: 2(4x + 6) – 5 = 8x + 7
17: 2(4x + 6) – 7 = 8x + 5
18: 2(4x + 6) – 9 = 8x + 3
19: 2(4x + 7) – 5 = 8x + 9
20: 2(4x + 7) – 9 = 8x + 5
21: 3(2x + 4) – 5 = 6x + 7
22: 3(2x + 4) – 7 = 6x + 5
23: 3(2x + 5) – 7 = 6x + 8
24: 3(2x + 5) – 8 = 6x + 7
25: 4(2x + 3) – 5 = 8x + 7
26: 4(2x + 3) – 7 = 8x + 5
Source: Will Case
 Open Middle®
Open Middle®



What I think is really cool about these problems about equivalent expressions is that even though there are multiple answers (and in this case, MANY answers), there are restrictions about where certain numbers can go in the expression – like, all of the samples posted have either a 2 or a 3 in the factor outside of the parentheses.
2(3x + 6) – 4 = 6x + 8
2(4x + 2) – 1 + 8x + 3
2 (3x + 8) – 7 = 6x + 9
2(3x+8)-7+6x+9