Open Middle®
Directions: Using the digits 1 to 9, at most one time each, place a digit in each box to create two true equations: one where the quotient is greater than 40 and one where it’s less than 40. You may reuse the same digits for each of the equations.
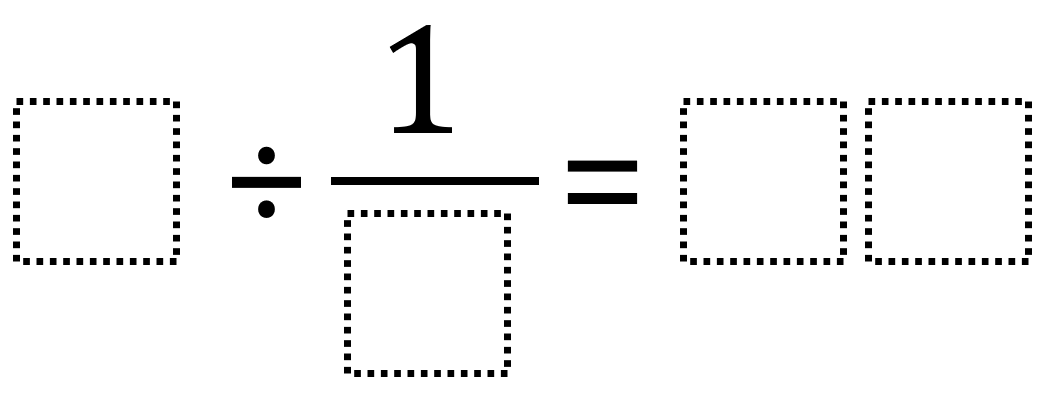
Hint
How can dividing by a single digit by a fraction result in a two-digit quotient?
Answer
There are many possible answers including 9 ÷ 1/3 = 27 and 9 ÷ 1/6 = 54.
Source: Robert Kaplinsky
Less : 3 divided by 1/2 = 6
More : 9 divided by 1/8 = 72
Here are all the solutions:
Less than 40:
2 ÷ 1/7 = 14
2 ÷ 1/8 = 16
2 ÷ 1/9 = 18
3 ÷ 1/4 = 12
3 ÷ 1/6 = 18
3 ÷ 1/7 = 21
3 ÷ 1/8 = 24
3 ÷ 1/9 = 27
4 ÷ 1/3 = 12
4 ÷ 1/7 = 28
4 ÷ 1/8 = 32
4 ÷ 1/9 = 36
6 ÷ 1/3 = 18
7 ÷ 1/2 = 14
7 ÷ 1/3 = 21
7 ÷ 1/4 = 28
8 ÷ 1/2 = 16
8 ÷ 1/3 = 24
8 ÷ 1/4 = 32
9 ÷ 1/2 = 18
9 ÷ 1/3 = 27
9 ÷ 1/4 = 36
Greater than 40:
6 ÷ 1/9 = 54
6 ÷ 1/7 = 42
7 ÷ 1/6 = 42
7 ÷ 1/8 = 56
7 ÷ 1/9 = 63
8 ÷ 1/7 = 56
8 ÷ 1/9 = 72
9 ÷ 1/6 = 54
9 ÷ 1/7 = 63
9 ÷ 1/8 = 72
less than 40:
3 ÷ 1/9 = 27
4 ÷ 1/3 = 12
4 ÷ 1/7 = 28
4 ÷ 1/8 = 32
4 ÷ 1/9 = 36
6 ÷ 1/3 = 18
7 ÷ 1/2 = 14
The soultions Less than 40:
2 ÷ 1/9 = 18
3 ÷ 1/4 = 12
3 ÷ 1/6 = 18
3 ÷ 1/7 = 21
3 ÷ 1/8 = 24
3 ÷ 1/9 = 27
4 ÷ 1/3 = 12
4 ÷ 1/7 = 28
4 ÷ 1/8 = 32
4 ÷ 1/9 = 36
6 ÷ 1/3 = 18
7 ÷ 1/2 = 14
7 ÷ 1/3 = 21
7 ÷ 1/4 = 28
8 ÷ 1/2 = 16
8 ÷ 1/3 = 24
8 ÷ 1/4 = 32
9 ÷ 1/2 = 18
9 ÷ 1/3 = 27
9 ÷ 1/4 = 36
2 ÷ 1/8 = 16
3 / 12 =1/4
8÷1/9=72
2÷1/3=6
0÷1/2=0
9%1/3=54