Directions: Using the digits 0 to 9 at most one time each, fill in the boxes to make a true equation.
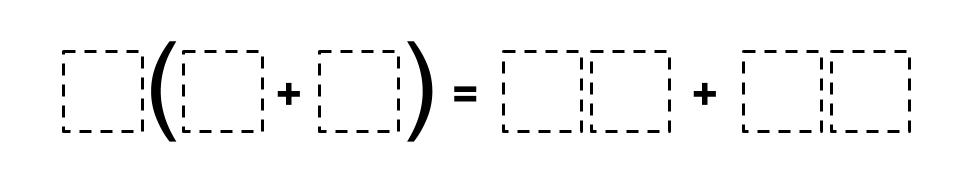
Hint
What number would be good/bad to distribute?
Answer
Number of Unique Solutions: 23
1: 2(3 + 9) = 06 + 18
2: 2(7 + 3) = 14 + 06
3: 3(9 + 6) = 27 + 18
4: 4(2 + 9) = 08 + 36
5: 4(5 + 9) = 20 + 36
6: 4(9 + 7) = 36 + 28
7: 6(3 + 7) = 18 + 42
8: 6(7 + 5) = 42 + 30
9: 6(9 + 3) = 54 + 18
10: 7(2 + 9) = 14 + 63
11: 7(3 + 8) = 21 + 56
12: 7(4 + 9) = 28 + 63
13: 7(8 + 2) = 56 + 14
14: 8(2 + 5) = 16 + 40
15: 8(3 + 7) = 24 + 56
16: 8(4 + 7) = 32 + 56
17: 8(9 + 5) = 72 + 40
18: 9(2 + 4) = 18 + 36
19: 9(2 + 6) = 18 + 54
20: 9(3 + 6) = 27 + 54
21: 9(4 + 8) = 36 + 72
22: 9(7 + 2) = 63 + 18
23: 9(8 + 6) = 72 + 54
1: 2(3 + 9) = 06 + 18
2: 2(7 + 3) = 14 + 06
3: 3(9 + 6) = 27 + 18
4: 4(2 + 9) = 08 + 36
5: 4(5 + 9) = 20 + 36
6: 4(9 + 7) = 36 + 28
7: 6(3 + 7) = 18 + 42
8: 6(7 + 5) = 42 + 30
9: 6(9 + 3) = 54 + 18
10: 7(2 + 9) = 14 + 63
11: 7(3 + 8) = 21 + 56
12: 7(4 + 9) = 28 + 63
13: 7(8 + 2) = 56 + 14
14: 8(2 + 5) = 16 + 40
15: 8(3 + 7) = 24 + 56
16: 8(4 + 7) = 32 + 56
17: 8(9 + 5) = 72 + 40
18: 9(2 + 4) = 18 + 36
19: 9(2 + 6) = 18 + 54
20: 9(3 + 6) = 27 + 54
21: 9(4 + 8) = 36 + 72
22: 9(7 + 2) = 63 + 18
23: 9(8 + 6) = 72 + 54
Source: Adrianne Burns
 Open Middle®
Open Middle®



My students absolutely LOVED doing this. We had an awesome follow up question: what is the lowest value for each expression you can get? What is the highest? Our lowest was 20. Our highest, 108. We had a lot of fun. Thanks for the challenge!
Ted, when you say “lowest value for each expression,” are you talking about the expression on either side of the equation? Because I’m puzzled how you could get 20, unless you allow a 2-digit number to start with 0. Otherwise, on the right, you’ll have a minimum of 1 ten plus 2 tens, or at least 30.
I like the idea of high/low, though! My lowest (for either side) is 45 and my highest is 126.
Thanks Ted and Julie. Ted, your version of the problem makes it a DOK 3 problem and you should definitely submit it to Open Middle using the link in the menu bar. That being said, definitely consider Julie’s feedback as it can be challenging writing the problem in such a way that it makes sense to virtually everyone.
So I did this with my class today to think about distributive property in solving equations (7th grade). I had a student think of this a little differently. Instead of the distributive property (which I know is a 6th grade standard and what this is written for) she thought of it as two equal expressions.
9(4+5) = 13 + 68
9(9) = 81
81 = 81
I love these. I’m trying to be better at starting my class with something that raises the rigor.
Just a quick question how does this type of mathematics apply to the real world?
4(3+6) = 09 +27 is correct but not on the answers.
Using the distributive property, I found 2(4+7)=03+19
If you allow leading zeros, there are 261 solutions (times 8, because you could swap the addends in the brackets, the units digits of the addends on the right or the tenths digits of the addends on the right.
2(3 + 7) = 04 + 16
2(3 + 8) = 05 + 17
2(3 + 9) = 06 + 18
2(4 + 6) = 03 + 17
2(4 + 7) = 03 + 19
2(4 + 8) = 05 + 19
2(5 + 6) = 03 + 19
2(5 + 6) = 04 + 18
2(5 + 7) = 06 + 18
2(5 + 8) = 07 + 19
3(1 + 9) = 04 + 26
3(2 + 5) = 04 + 17
3(2 + 6) = 05 + 19
3(2 + 7) = 08 + 19
3(4 + 5) = 01 + 26
3(4 + 5) = 08 + 19
3(4 + 6) = 01 + 29
3(4 + 7) = 05 + 28
3(4 + 8) = 07 + 29
3(4 + 8) = 10 + 26
3(5 + 6) = 04 + 29
3(5 + 7) = 10 + 26
3(5 + 8) = 10 + 29
3(5 + 9) = 14 + 28
3(6 + 7) = 10 + 29
3(6 + 7) = 14 + 25
3(6 + 8) = 15 + 27
3(6 + 9) = 17 + 28
3(7 + 8) = 16 + 29
3(7 + 9) = 02 + 46
3(8 + 9) = 05 + 46
4(1 + 6) = 03 + 25
4(1 + 7) = 03 + 29
4(1 + 8) = 07 + 29
4(1 + 9) = 02 + 38
4(2 + 7) = 01 + 35
4(2 + 8) = 01 + 39
4(2 + 9) = 06 + 38
4(3 + 6) = 07 + 29
4(3 + 8) = 15 + 29
4(5 + 7) = 10 + 38
4(5 + 7) = 12 + 36
4(5 + 9) = 20 + 36
4(6 + 8) = 17 + 39
4(6 + 8) = 21 + 35
4(6 + 9) = 02 + 58
4(6 + 9) = 03 + 57
4(7 + 8) = 01 + 59
4(7 + 8) = 21 + 39
4(7 + 9) = 01 + 63
4(7 + 9) = 06 + 58
4(7 + 9) = 26 + 38
4(8 + 9) = 01 + 67
4(8 + 9) = 03 + 65
4(8 + 9) = 12 + 56
5(0 + 8) = 13 + 27
5(0 + 8) = 14 + 26
5(0 + 9) = 17 + 28
5(1 + 6) = 07 + 28
5(1 + 7) = 02 + 38
5(1 + 7) = 04 + 36
5(1 + 8) = 02 + 43
5(1 + 8) = 06 + 39
5(1 + 9) = 02 + 48
5(1 + 9) = 03 + 47
5(2 + 3) = 06 + 19
5(2 + 3) = 07 + 18
5(2 + 6) = 01 + 39
5(2 + 7) = 06 + 39
5(2 + 8) = 01 + 49
5(2 + 8) = 03 + 47
5(2 + 8) = 14 + 36
5(2 + 9) = 07 + 48
5(2 + 9) = 17 + 38
5(3 + 4) = 06 + 29
5(3 + 4) = 07 + 28
5(3 + 6) = 17 + 28
5(3 + 7) = 01 + 49
5(3 + 7) = 02 + 48
5(3 + 8) = 06 + 49
5(3 + 9) = 12 + 48
5(4 + 6) = 12 + 38
5(4 + 7) = 16 + 39
5(4 + 8) = 21 + 39
5(4 + 9) = 02 + 63
5(4 + 9) = 27 + 38
5(6 + 8) = 21 + 49
5(6 + 8) = 23 + 47
5(6 + 9) = 01 + 74
5(6 + 9) = 02 + 73
5(6 + 9) = 27 + 48
5(7 + 8) = 12 + 63
5(7 + 8) = 26 + 49
5(7 + 9) = 12 + 68
5(7 + 9) = 32 + 48
5(8 + 9) = 12 + 73
5(8 + 9) = 21 + 64
6(0 + 7) = 13 + 29
6(0 + 7) = 14 + 28
6(1 + 4) = 03 + 27
6(1 + 5) = 02 + 34
6(1 + 5) = 07 + 29
6(1 + 7) = 03 + 45
6(1 + 8) = 05 + 49
6(1 + 8) = 20 + 34
6(1 + 9) = 02 + 58
6(1 + 9) = 03 + 57
6(2 + 4) = 01 + 35
6(2 + 5) = 04 + 38
6(2 + 7) = 01 + 53
6(2 + 7) = 05 + 49
6(2 + 7) = 15 + 39
6(2 + 8) = 01 + 59
6(2 + 8) = 03 + 57
6(2 + 8) = 13 + 47
6(3 + 4) = 15 + 27
6(3 + 5) = 01 + 47
6(3 + 7) = 01 + 59
6(3 + 7) = 02 + 58
6(3 + 7) = 12 + 48
6(3 + 8) = 07 + 59
6(3 + 8) = 12 + 54
6(3 + 8) = 17 + 49
6(3 + 8) = 21 + 45
6(3 + 9) = 14 + 58
6(3 + 9) = 25 + 47
6(4 + 8) = 13 + 59
6(4 + 9) = 03 + 75
6(4 + 9) = 20 + 58
6(4 + 9) = 21 + 57
6(5 + 7) = 23 + 49
6(5 + 7) = 30 + 42
6(5 + 8) = 31 + 47
6(5 + 9) = 01 + 83
6(5 + 9) = 10 + 74
6(7 + 8) = 31 + 59
6(7 + 9) = 12 + 84
6(8 + 9) = 30 + 72
7(0 + 6) = 13 + 29
7(0 + 6) = 14 + 28
7(0 + 8) = 21 + 35
7(0 + 9) = 15 + 48
7(0 + 9) = 25 + 38
7(1 + 4) = 06 + 29
7(1 + 5) = 04 + 38
7(1 + 8) = 04 + 59
7(1 + 8) = 20 + 43
7(1 + 8) = 24 + 39
7(1 + 9) = 02 + 68
7(2 + 5) = 01 + 48
7(2 + 5) = 03 + 46
7(2 + 5) = 10 + 39
7(2 + 8) = 01 + 69
7(2 + 8) = 14 + 56
7(2 + 9) = 13 + 64
7(2 + 9) = 31 + 46
7(3 + 5) = 10 + 46
7(3 + 6) = 04 + 59
7(3 + 6) = 15 + 48
7(3 + 8) = 12 + 65
7(3 + 8) = 21 + 56
7(3 + 9) = 20 + 64
7(3 + 9) = 26 + 58
7(4 + 5) = 01 + 62
7(4 + 6) = 12 + 58
7(4 + 8) = 15 + 69
7(4 + 8) = 21 + 63
7(4 + 9) = 05 + 86
7(4 + 9) = 23 + 68
7(4 + 9) = 30 + 61
7(5 + 6) = 28 + 49
7(5 + 8) = 30 + 61
7(5 + 9) = 12 + 86
7(5 + 9) = 30 + 68
7(6 + 8) = 03 + 95
7(6 + 9) = 20 + 85
7(6 + 9) = 21 + 84
8(0 + 5) = 13 + 27
8(0 + 5) = 14 + 26
8(0 + 7) = 21 + 35
8(0 + 9) = 25 + 47
8(1 + 3) = 05 + 27
8(1 + 5) = 02 + 46
8(1 + 6) = 02 + 54
8(1 + 6) = 07 + 49
8(1 + 7) = 25 + 39
8(1 + 9) = 04 + 76
8(1 + 9) = 23 + 57
8(1 + 9) = 24 + 56
8(2 + 5) = 07 + 49
8(2 + 5) = 10 + 46
8(2 + 5) = 17 + 39
8(2 + 6) = 10 + 54
8(2 + 6) = 15 + 49
8(2 + 7) = 03 + 69
8(2 + 7) = 13 + 59
8(2 + 9) = 13 + 75
8(2 + 9) = 31 + 57
8(3 + 6) = 25 + 47
8(3 + 7) = 21 + 59
8(3 + 7) = 24 + 56
8(3 + 9) = 20 + 76
8(3 + 9) = 21 + 75
8(3 + 9) = 40 + 56
8(4 + 5) = 03 + 69
8(4 + 5) = 10 + 62
8(4 + 6) = 01 + 79
8(4 + 6) = 21 + 59
8(4 + 6) = 23 + 57
8(4 + 7) = 23 + 65
8(4 + 7) = 32 + 56
8(5 + 7) = 02 + 94
8(5 + 7) = 32 + 64
8(5 + 9) = 40 + 72
8(6 + 7) = 10 + 94
9(0 + 5) = 17 + 28
9(0 + 7) = 15 + 48
9(0 + 7) = 25 + 38
9(0 + 8) = 25 + 47
9(1 + 4) = 07 + 38
9(1 + 5) = 06 + 48
9(1 + 5) = 20 + 34
9(1 + 6) = 20 + 43
9(1 + 6) = 25 + 38
9(1 + 7) = 04 + 68
9(1 + 7) = 30 + 42
9(1 + 8) = 05 + 76
9(1 + 8) = 24 + 57
9(1 + 8) = 35 + 46
9(2 + 4) = 01 + 53
9(2 + 4) = 16 + 38
9(2 + 5) = 16 + 47
9(2 + 6) = 14 + 58
9(2 + 7) = 13 + 68
9(2 + 7) = 30 + 51
9(2 + 7) = 35 + 46
9(2 + 8) = 14 + 76
9(2 + 8) = 34 + 56
9(3 + 4) = 01 + 62
9(3 + 4) = 06 + 57
9(3 + 5) = 04 + 68
9(3 + 5) = 10 + 62
9(3 + 6) = 24 + 57
9(3 + 7) = 04 + 86
9(3 + 8) = 24 + 75
9(3 + 8) = 42 + 57
9(4 + 5) = 03 + 78
9(4 + 5) = 13 + 68
9(4 + 5) = 20 + 61
9(4 + 6) = 03 + 87
9(4 + 6) = 12 + 78
9(4 + 6) = 32 + 58
9(4 + 7) = 13 + 86
9(4 + 7) = 31 + 68
9(4 + 8) = 32 + 76
9(5 + 6) = 12 + 87
9(5 + 6) = 21 + 78
9(5 + 7) = 40 + 68
9(5 + 8) = 41 + 76
9(6 + 7) = 32 + 85
9(6 + 8) = 52 + 74
So the solution section is missing a lot of solutions, like for example 2*(3 + 8) = 05 + 17. There’s nothing even remotely equivalent to it in the solution section. There’s not one solution that contains the digits 2, 3, 8, 0, 5, 1, 7 in any order. There’s not even one that results in 22. Same goes for many others.
Since some users were wondering:
The highest result is indeed 126 = 9(6 + 8) = 52 + 74
The lowest result is 20 = 2(3 + 7) = 04 + 16 or 20 = 2(4 + 6) = 03 + 17. Without leading zeros, it’s
36 = 3(4 + 8) = 10 + 26 or 36 = 3(5 + 7) = 10 + 26
Side note: 151 of the 261 solutions have no leading zeros.