Open Middle®
Directions: Using the digits 0 to 9 at most one time each, place a digit in each box to make both expressions factorable.
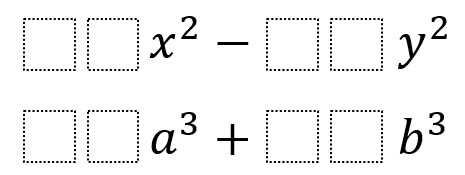
Hint
How can we write rewrite the expressions such that (##a)^3 is equivalent to ☐☐*a^3?
If you can only find a few solutions, have you considered expressions where you first factor out the GCF?
Answer
81, 09 and 64, 27
36, 49 and 01, 27
25, 36 and 64, 01
36, 49 and 01, 27
25, 36 and 64, 01
There are a lot (not infinite) of solutions once you include taking out the GCF.
For example:
36x^2 – 09y^2 –> 9(4x^2 -1y^2) –> factorable!
and
81a^3 + 24b^3 –> 3(27a^3 + 8b^3) –> factorable!
Source: Jack Assaf
A question might be what does factorable mean z
01x^2-23y^2=
(x+y*23^.5)(x-y*23^.5) if it meets the definition of factorable.
Question is can we factor
x^2-i^2?
There is some importance to consider this topic since an approach to solving all quadratics is to slide function so axis of symmetry and the linear coefficient always becomes 0 meaning solutions ( real and non real) can be found by factoring with difference of squares pattern. Set linear factors to zero and solve.
You can also use 08 as a perfect cube.