Directions: Directions: Using the digits 0 to 9, at most one time each, fill in the boxes to create numbers on the number line.
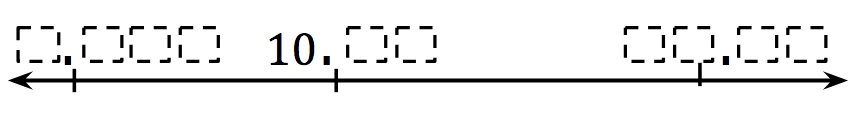
Hint
What is the difference of [that number] and the 10? How could you make [number] greater or less?
Answer
There are many correct solutions: 7.34, 10.890, 12.56; 6.78, 10.349, 15.02; and 0.13, 10.987, 26.45 are three examples. There are not infinite correct answers.
Source: Anne Oliveira
 Open Middle®
Open Middle®

There are 10! ways to map the 10 digits to the 10 boxes, but while the number on the left will always be less than 10, the number on the right is not always bigger than the middle one. So we have to subtract the number of ways where the middle number is greater than or equal to the right number, which can only be the case if the number on the right has a 1 in the tens place and a 0 in the ones place (or the tens place is a one, but I’ll comment on that later) and the decimals of the second number are bigger than the decimals of third number. These conditions are met in 727 cases (more specifically: there are 727 cases of two numbers of the form 10.ab and 10.cd where ab < cd and a,b,c,d are four different digits between 2 and 9), which has to be multiplied by 4*3*2*1, because of the four digits left for the first number, giving us a total of 17,448 possible ways to put the 10 digits in the 10 boxes where the inequalities don't hold.
So there are 10! – 17,448 = 3,628,800 – 17,448 = 3,611,352 ways to solve the problem above. More than 99,5% of the 3,628,800 permutations of the digits 0 through 9 are solutions to the problem above.
However, this includes solutions where the tens place of the right number is a 0 and solutions where the last decimal place written is a 0 (like 9.210 < 10.34 < 56.78 or 1.234 < 10.56 < 78.90). There are 9! = 362,880 solutions with a 0 in the tens place of the right number, so subtracting those there are 3,248,472 solutions. Subtracting 3*9! = 1,088,640 solutions with a 0 as the last decimal place written, we are left with 2,159,832 solutions. Even with these restrictions, almost 60% of the 3,628,800 permutations of the digits 0 through 9 are solutions to the problem.
In order to get easy solutions, just use 4 different digits that make a number >11 on the right and afterwards distribute the remaining 6 digits however you like.
Or – for the harder to find solutions – use the digits 1 and 0 in the tens and ones place of the number on the right and find one of the 727 solutions where the number on the right is bigger than the middle number and distribute the remaining 4 digits to the first number however you like.