Directions: Use the operation symbols (+, -, x, ÷) and equal sign (=) to make a true equation. Operation symbols may be used more than once.
What is the least value for each part of the equation? What is the greatest value for each part of the equation?
Can you complete the equation with at least one of each symbol?
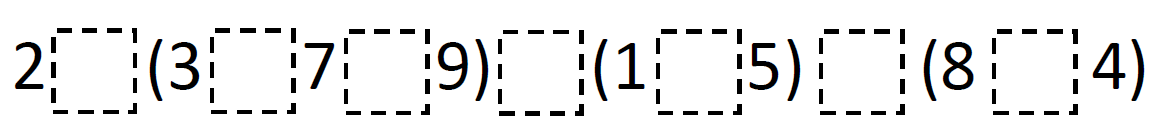
Hint
Where might you place the equals sign(s)?
Answer
Several answers are possible such as 2 x (3 + 7 – 9) x (1 + 5) = (8 + 4)
2 x (3 + 7 + 9) = (1 + 5) + (8 x 4)
2 x (3 + 7 + 9) = (1 + 5) + (8 x 4)
Using each symbol at least once, here is one solution: 2=(3×7-9)/(1+5)=(8/4)
Source: Joshua Nelson and Renee Owen
 Open Middle®
Open Middle®



2-(3+7-9)=(1+5)-(8-4)
There are 48 solutions:
2 = (3 + 7 – 9) – (1 – 5) / (8 – 4)
2 + (3 + 7 – 9) = (1 * 5) – (8 / 4)
2 = (3 + 7 – 9) + (1 * 5) – (8 – 4)
2 – (3 + 7 – 9) = (1 * 5) – (8 – 4)
2 + (3 + 7 – 9) = (1 + 5) / (8 / 4)
2 = (3 + 7 – 9) / (1 + 5) * (8 + 4)
2 * (3 + 7 – 9) * (1 + 5) = (8 + 4)
2 / (3 + 7 – 9) * (1 + 5) = (8 + 4)
2 = (3 + 7 – 9) * (1 + 5) – (8 – 4)
2 * (3 + 7 – 9) = (1 + 5) – (8 – 4)
2 / (3 + 7 – 9) = (1 + 5) – (8 – 4)
2 = (3 – 7 * 9) / (1 + 5) + (8 + 4)
2 – (3 – 7 * 9) / (1 + 5) = (8 + 4)
2 = (3 – 7 + 9) * (1 / 5) * (8 / 4)
2 / (3 – 7 + 9) = (1 / 5) * (8 / 4)
2 * (3 – 7 + 9) * (1 / 5) = (8 / 4)
2 / (3 – 7 + 9) / (1 / 5) = (8 / 4)
2 = (3 – 7 + 9) – (1 * 5) + (8 / 4)
2 = (3 – 7 + 9) / (1 * 5) * (8 / 4)
2 + (3 – 7 + 9) = (1 * 5) + (8 / 4)
2 * (3 – 7 + 9) = (1 * 5) * (8 / 4)
2 – (3 – 7 + 9) + (1 * 5) = (8 / 4)
2 + (3 – 7 + 9) – (1 * 5) = (8 / 4)
2 / (3 – 7 + 9) * (1 * 5) = (8 / 4)
2 * (3 – 7 + 9) / (1 * 5) = (8 / 4)
2 + (3 – 7 + 9) + (1 * 5) = (8 + 4)
2 + (3 – 7 + 9) * (1 + 5) = (8 * 4)
2 = (3 – 7 + 9) – (1 + 5) / (8 / 4)
2 * (3 – 7 + 9) = (1 + 5) + (8 – 4)
2 * (3 – 7 + 9) – (1 + 5) = (8 – 4)
2 = (3 * 7 / 9) + (1 – 5) / (8 + 4)
2 – (3 * 7 / 9) = (1 – 5) / (8 + 4)
2 = (3 * 7 / 9) * (1 + 5) – (8 + 4)
2 = (3 * 7 – 9) – (1 * 5) * (8 / 4)
2 = (3 * 7 – 9) – (1 + 5) – (8 – 4)
2 * (3 * 7 – 9) = (1 + 5) * (8 – 4)
2 + (3 * 7 – 9) / (1 + 5) = (8 – 4)
2 * (3 * 7 – 9) / (1 + 5) = (8 – 4)
2 = (3 + 7 + 9) – (1 * 5) – (8 + 4)
2 * (3 + 7 + 9) = (1 + 5) + (8 * 4)
2 * (3 + 7 + 9) – (1 + 5) = (8 * 4)
2 * (3 – 7 – 9) = (1 + 5) – (8 * 4)
2 * (3 * 7 + 9) * (1 / 5) = (8 + 4)
2 = (3 * 7 + 9) * (1 / 5) – (8 – 4)
2 = (3 * 7 + 9) – (1 – 5) – (8 * 4)
2 * (3 * 7 + 9) = (1 * 5) * (8 + 4)
2 * (3 * 7 + 9) / (1 * 5) = (8 + 4)
2 = (3 * 7 + 9) / (1 * 5) – (8 – 4)
The lowest (and at the same time greatest negative integer) result for each part of the equation is -26 = 2 * (3 – 7 – 9) = (1 + 5) – (8 * 4)
The greatest result for each part of the equation is 60 = 2 * (3 * 7 + 9) = (1 * 5) * (8 + 4)
The lowest positive result for each part of the equation is 0.4 = 2 / (3 – 7 + 9) = (1 / 5) * (8 / 4)
The greatest negative result for each part of the equation is -0.33 = 2 – (3 * 7 / 9) = (1 – 5) / (8 + 4)
The lowest positive integer result for each part of the equation is 1 = 2 – (3 + 7 – 9) = (1 * 5) – (8 – 4)
Other possible results are 2, 3, 4, 7, 10, 12, 24, 32, 38
There are a few equivalent equations among them:
For example, 2 + (3 + 7 – 9) = (1 * 5) – (8 / 4) is equivalent to 2 – (3 + 7 – 9) = (1 * 5) – (8 – 4)
If we calculate the result of the expressions in brackets first:
6 of the 40 solutions require negative numbers, but no decimal numbers/fractions, for example 2 = (3 * 7 + 9) – (1 – 5) – (8 * 4)
7 of the 40 solutions require decimal numbers/fractions, but no negative numbers, for example 2 * (3 – 7 + 9) * (1 / 5) = (8 / 4)
2 of the 40 solutions require both negative and decimal numbers/fractions:
2 = (3 * 7 / 9) + (1 – 5) / (8 + 4) and 2 – (3 * 7 / 9) = (1 – 5) / (8 + 4)
The other 25 solutions require neither negative nor decimal numbers/fractions, for example 2 + (3 + 7 – 9) = (1 * 5) – (8 / 4).
23 solutions contain each operation symbol at least once:
2 + (3 + 7 – 9) = (1 * 5) – (8 / 4)
2 = (3 + 7 – 9) / (1 + 5) * (8 + 4)
2 / (3 + 7 – 9) * (1 + 5) = (8 + 4)
2 = (3 – 7 * 9) / (1 + 5) + (8 + 4)
2 – (3 – 7 * 9) / (1 + 5) = (8 + 4)
2 = (3 – 7 + 9) * (1 / 5) * (8 / 4)
2 / (3 – 7 + 9) = (1 / 5) * (8 / 4)
2 * (3 – 7 + 9) * (1 / 5) = (8 / 4)
2 = (3 – 7 + 9) – (1 * 5) + (8 / 4)
2 = (3 – 7 + 9) / (1 * 5) * (8 / 4)
2 + (3 – 7 + 9) = (1 * 5) + (8 / 4)
2 * (3 – 7 + 9) = (1 * 5) * (8 / 4)
2 – (3 – 7 + 9) + (1 * 5) = (8 / 4)
2 + (3 – 7 + 9) – (1 * 5) = (8 / 4)
2 / (3 – 7 + 9) * (1 * 5) = (8 / 4)
2 * (3 – 7 + 9) / (1 * 5) = (8 / 4)
2 = (3 * 7 / 9) + (1 – 5) / (8 + 4)
2 – (3 * 7 / 9) = (1 – 5) / (8 + 4)
2 = (3 * 7 / 9) * (1 + 5) – (8 + 4)
2 + (3 * 7 – 9) / (1 + 5) = (8 – 4)
2 * (3 * 7 – 9) / (1 + 5) = (8 – 4)
2 = (3 * 7 + 9) * (1 / 5) – (8 – 4)
2 = (3 * 7 + 9) / (1 * 5) – (8 – 4)
Out of these, if we calculate the result of the expressions in brackets first:
4 of the 23 solutions require negative numbers, but no decimal numbers/fractions, for example 2 = (3 – 7 * 9) / (1 + 5) + (8 + 4)
5 of the 23 solutions require decimal numbers, but no negative numbers/fractions, for example 2 * (3 – 7 + 9) * (1 / 5) = (8 / 4)
2 of the 23 solutions require both negative and decimal numbers:
2 = (3 * 7 / 9) + (1 – 5) / (8 + 4) and 2 – (3 * 7 / 9) = (1 – 5) / (8 + 4)
The other 12 solutions require neither negative nor decimal numbers/fractions, for example 2 + (3 + 7 – 9) = (1 * 5) – (8 / 4)
—
If it wasn’t an equation, but just an expression (so no “=” sign), then in total, there would be 4^7 = 16,384 possible expressions.
The smallest result possible is 2 * (3 * 7 * 9) * (1 – 5) * (8 * 4) = -48,384
The greatest result smaller than 0 is 2 / (3 * 7 * 9) / (1 – 5) / (8 * 4) = -8,2(67195)*10^(-5)
The greatest integer result smaller than 0 is -1, for example as the result of 2 + (3 – 7 + 9) + (1 – 5) – (8 – 4)
The smallest positive result is 2 / (3 * 7 * 9) / (1 + 5) / (8 * 4) = 5,(511463844797178130)*10^(-5)
The smallest positive integer result is 1, for example as the result of 2 – (3 + 7 – 9) + (1 – 5) + (8 / 2)
The greatest result possible is 2 * (3 * 7 * 9) * (1 + 5) * (8 * 4) = 72,576
There are 4,597 whole-numbered results. 83 is the smallest positive integer that can not be gotten with any combination of the 4 operators. 91, 103, 107, 113, 121, 127, 137, 145, 147, 151, 172, 177, 205, 221, 223, 225, 231, 233, 235, 236, 237, 241, 243, 245, 247, 249, 253, 255, 257, 258, 259, 261 and many more integers can also never be the result.
There are 8400 expressions with at least 1 of each operation symbol.
Wow, that is incredible! Thanks for dedicating the time to working out this task so thoroughly. You’ve taken SMP 1 (Make sense of problems and persevere in solving them) to a whole other level Rudolf Österreicher!