Directions: Using the integers -9 to 9 at most one time each, fill in the boxes to create coordinates that represent the vertices of the triangle with the smallest possible area.
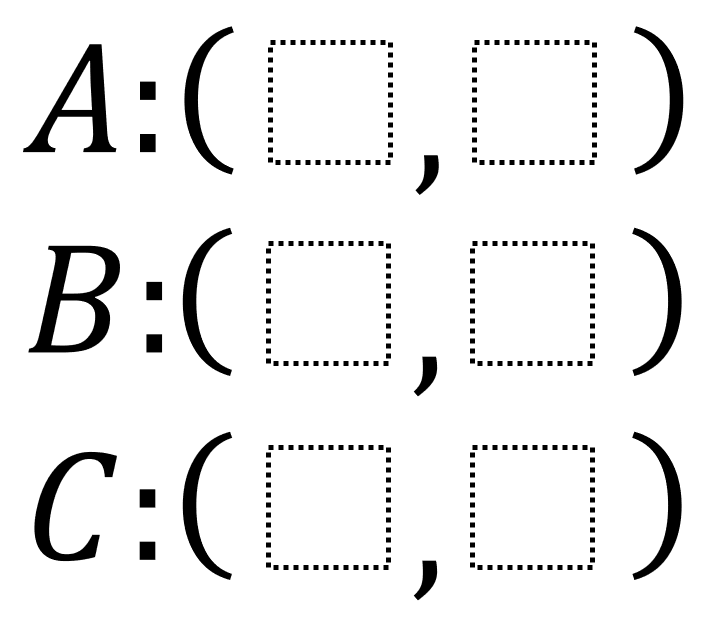
Hint
How can you graphically estimate your triangle’s area before you calculate it?
Answer
The triangle with the smallest possible area that has been found so far has an area of 2.5 units2 from the coordinates (-1, 1), (0, 2), and (1, -2). If you find one with less area, share it in the comments.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®

In the answer given, integer 1 was used twice. I thought this wasn’t allowed.
I have a student who found coordinates that result in a triangle with area of .5 square units.
A (4, 5)
B (3, 6)
C (2, 8)
Said student not having learned the matrix determinant yet, we used the calculator at https://www.had2know.com/academics/triangle-area-perimeter-angle-3-coordinates.html#:~:text=The%20area%20of%20a%20triangle%20given%20by%20a,rows%20%28or%20columns%29%20%5Ba-e%2C%20b-f%5D%20and%20%5Bc-e%2C%20d-f%5D.
to determine the area of the triangle.
You don’t need a calculator to solve this if you use a coordinate grid. If you box off a small section of a coordinate grid around with the coordinates (1,0), (3,1), (1,3) and (3, 3) You create a 2×3 box having an area of 6 units squared.
The coordinates for the triangle are (1,0), (2, -1), (3, -3). The right triangle formed at the bottom left is 3 square units (5 * 2 * 3). The coordinate @ (2, -1) then allows you to have a whole box in the upper right corner with an area of 1 square unit. This box allows you to form two more right triangles which you can find the area of. (.5 * 1 * 1) = .5 square units. (.5 * 2 * 1) = 1 square unit. Subtract the areas from that of the box 6 – 3 – 1 – .5 = .5 units squared.
A(1,0)
B(2, -1)
C(3,-3)