Directions: Using the digits 0 to 9 at most one time each, fill in the blanks to create a quadrilateral with an area of 16 square units.
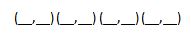
Hint
What happens if two ordered pairs have the same x-value?
What happens if two ordered pairs have the same y-value?
What happens if two ordered pairs have the same y-value?
Answer
One solution is (1,2), (3,0), (5,6), (7,4). Note: If you change the range of integers to be -9 to 9, then the question is also aligned to standard 6.NS.6b.
Source: Daniel Luevanos
 Open Middle®
Open Middle®



I am not sure that I agree that this problem is aligned with 6th grade standards. I believe that given the coordinates, 6th graders should be able to compose a larger rectangle by drawing 4 right triangles surrounding the graphed quadrilateral. The resultant rectangle would have coordinates with same first or last coordinates and its area could be found. Students could also find the area of the right triangles and subtract those from the larger rectangle to find the area of the original graphed rectangle. This would correlate with CCSS 6.G.3 I might also change the challenge to allow use of integers between -9 and 9 and allowing them to repeat which would also align with G.1 and G.3 Do you have any other suggestions or is my understanding faulty?
I really like this site and the problems.
Thank you.
Great suggestion. I can see how this question could be aligned to 6.G.3. If you did change the range of numbers to be -9 to 9, then the question can also be aligned to 6.NS.6b. Glad you like the questions on the website too! This is one of my favorite websites!
C Farmer, if you are saying it would be very difficult for a 6th grader (pre-Pythagorean Thm) to construct the rectangle to meet the conditions, but that it is reasonable for them to come up with a way to figure out the area for this particular solution, then I agree. Or maybe you’re suggesting giving them the surrounding square and having them carve off right triangles?
My sixth grade students successfully reached an answer to this problem today! They are immensely proud of themselves, and I am immensely proud of their perseverance — this problem spanned multiple math periods for us. They propose these coordinates: (3,6), (8,5), (7,2), (1,4). Thank you for challenging my students!
This is so awesome, Kimberly! Thank you for sharing! Great work, kids!
When we have plotted these points on a Cartesian Plane we have gotten the rectangle, however why does the formula for square units of area not seem to be able to be applied. We have a length of 4 but only a width of 2 units?? Please help!
I get a 2 unit by 4 unit rectangle, as well, when I plot the ordered pairs for the given answer. This would give an area of 8 square units. Am I missing something?
I know I am like fives years too late, but if you plot the points of the given answer you will have a rectangle that has been twisted so the length and width are not perpendicular to the horizontal or vertical axis. To find the length and the width you must apply the Pythagorean theorem a^2+b^2 = c^2 when this theorem is applied you will get that the width and the length of the rectangle is √8 and √32 not 2 and 4. √8 x √32= 16
I am looking for clarification on this. Are the students expected to know Pythagorean Theorem, to identify the hypotenuse for each triangle? Or are they supposed to draw the rectangular shape and then find the area of each resulting triangle, and subtract from the original area?
i do not really get it can u please help me?
What happens if two ordered pairs have the same x-value? The same with y-value
What happened to the X and the Y value are both negative numbers
1.2 3.4 5.2 3.0
0,1,2,3,4,5,6.7.8.9.
0,1,2,3,4,5,6,7
Aylin is a 6th grader at QVMS. I am her father and trying to understand and solve the problem above. We could not figure it out ourselves. But we looked at the proposed solution above by Mrs. Kimberly. We did understand how they did this by using a coordinate system on our board at home. It is a challenging but a great question we think. The way we think Kimberley’s students reach a solution is that they drew a shape of a rectangle on the coordinate system in 16 unit square and rotate it/twisted or manipulated the shape into a shape (keeping the total area fixed) at the coordinate locations that are using numbers 1 thru 9, but not repeating any number. Great exercise. Thank you for the challenge.
0,1,2,3,4,5,6,7,8,9
just to be are we supposed to post this some where
1,2 3,0 5,6 7,4
1 2 3 0 5 6 7 4
the answer is (1,2)(3,0)(5,6)(7,4)
1*2 1*2 1*2 1*2
(1,2)
1,2 3,0 5,6 7,4
123056574
(1.2)(3,0)(5,6)(7,4)
(1,2)(3,0)(5,6)(7,4)
(1,2) (3,0) (5,6) (7,4)
(1,1) (1,5) (4,1) (4,5)
(1,2), (3,0), (5,6), (7,4)
i think it is 1.2 3.4 5.2 3.0
i think its– 1,2 3,0 5,6 7,4
I think it’s this 1, 2 3,0 5, 6 7,4
I think it is 1, 2 3,0 5, 6 7,4
the answer is (1,2)(3,0)(5,6)(7,4)
I think its 1,2 3,0 5,6 7,4
i believe that its 1,2 3,0 5,6 7,4
[1,2] [3,0] [5,6] [7,4]
(1,2) (3,0) (5,6) (7,4)
1,2 3,0 5,6 7,4
The answer is(1,2), (3,0) , (5,6) , (7,4)
1,2,3,0,5,6,7,4
01234456.7.8.9
Even restricting ourselves to the integers between 0 and 9, there are 25,536 solutions (so unfortunately way too many to list here):
128 rectangles (p.e. (9,6), (7,8), (3,4), (5,2))
272 convex kites that are not rhombi (p.e. (9,6), (4,7), (5,2), (8,3))
32 rhombi (p.e. (9,0), (6,5), (1,8), (4,3))
80 concave kites that are not rhombi (p.e. (9,0), (2,3), (5,4), (6,7))
32 concave trapezoids that are not parallelogramms (p.e. (8,6), (2,0), (3,9), (1,7))
12,400 convex irregular quadrilaterals (p.e. (9,8), (7,5), (4,2), (0,3))
12,592 concave irregular quadrilaterals (p.e. (9,8), (7,6), (5,0), (2,4))
No squares, no convex trapezoids and no parallelogramms that are not rhombi.
Note: When I say irregular quadrilateral, I actually mean a quadrilateral that is neither a trapezoid nor a kite (and therefore isn’t a parallelogramm, a rhombus, a square or a rectangle either). Maybe “general quadrilateral” is a better term?
However, you can divide the number of solutions by 8 because:
If you have points A, B, C, D, then
– the quadrilateral (A, B, C, D) is the same as the quadrilaterals (B, C, D, A), (C, D, A, B), (D, A, B, C) as well as…
– (D, C, B, A), (A, D, C, B), (B, A, D, C) and (C, B, A, D)
Also, if A=(x(A), y(A)), B=(x(B), y(B)), C=(x(C), y(C)), D=(x(D), y(D)) is a solution, so is the quadrilateral that is mirrored along the line y=x, resulting in a quadrilateral whose vertices have the coordinates A=(y(A), x(A)), B=(y(B), x(B)), C=(y(C), x(C)), D=(y(D), x(D)), or in short: The x- and y-coordinates are swapped. For example: both (9,8), (6,3), (1,0), (4,5)
and (8,9), (3,6), (0,1), (5,4) are solutions. If you don’t count these as unique solutions, these are the numbers of unique solutions:
8 rectangles
17 convex kites that are not rhombi
2 rhombi
5 concave kites that are not rhombi
2 concave trapezoids that are not parallelogramms
775 convex general quadrilaterals
787 concave general quadrilaterals
Here are all the unique solutions (and by swapping the x- and y-coordinates, you get twice as many solutions) except for the 775+787 general quadrilaterals:
Rhombi:
(9,8), (6,3), (1,0), (4,5) and (9,0), (6,5), (1,8), (4,3)
Convex kites that are not rhombi:
(7,0), (6,5), (3,4), (2,1)
(7,1), (6,4), (3,5), (2,0)
(7,4), (6,1), (3,0), (2,5)
(7,5), (6,0), (3,1), (2,4)
(8,1), (7,6), (4,5), (3,2)
(8,2), (7,5), (4,6), (3,1)
(8,5), (7,2), (4,1), (3,6)
(8,6), (7,1), (4,2), (3,5)
(9,0), (4,7), (1,8), (2,5)
(9,0), (5,6), (1,8), (3,4)
(9,0), (7,4), (1,8), (5,2)
(9,2), (8,7), (5,6), (4,3)
(9,3), (8,6), (5,7), (4,2)
(9,6), (8,3), (5,2), (4,7)
(9,7), (8,2), (5,3), (4,6)
(9,8), (5,2), (1,0), (3,4)
(9,8), (7,4), (1,0), (5,6)
Rectangles:
(9,6), (7,8), (3,4), (5,2)
(9,4), (7,6), (3,2), (5,0)
(9,4), (7,2), (3,6), (5,8)
(9,2), (7,0), (3,4), (5,6)
(8,5), (6,7), (2,3), (4,1)
(8,3), (6,1), (2,5), (4,7)
(7,4), (3,0), (1,2), (5,6)
(7,2), (5,0), (1,4), (3,6)
Concave kites that are not rhombi:
(0,1), (5,4), (8,9), (7,2)
(0,9), (3,2), (4,5), (7,6)
(0,6), (3,5), (4,2), (7,9)
(0,5), (3,6), (4,9), (7,2)
(0,2), (3,9), (4,6), (7,5)
Concave trapezoids that are not parallelogramms:
(9,7), (3,1), (2,8), (0,6) and (9,3), (7,1), (6,8), (0,2)
If you change the range of integers to -9 to 9 (and you can use both a and -a in the same solution), there are 1,108,857 unique solutions. This number…
– exludes (B, C, D, A), (C, D, A, B), (D, A, B, C), (D, C, B, A), (A, D, C, B), (B, A, D, C) and (C, B, A, D) if (A, B, C, D) is a solution (which would just be equivalent to a change of the names of the vertices)
– exludes quadrilaterals that are just mirrors of any of the x solutions along the lines y=x or y=-x or the origin, because if (x(A), y(A)), (x(B), y(B)), (x(C), y(C)), (x(D), y(D)) is a solution, then the quadrilateral mirrored across the origin (-x(A), -y(A)), (-x(B), -y(B)), (-x(C), -y(C)), (-x(D), -y(D)) and the quadrilateral mirrored across the line y=-x, (-y(A), -x(A)), (-y(B), -x(B)), (-y(C), -x(C)), (-y(D), -x(D)) as well as the quadrilateral mirrored across the line y=-x, (y(A), x(A)), (y(B), x(B)), (y(C), x(C)), (y(D), x(D)) are also solutions.
Among these 1,108,857 solutions, there are…
86 rectangles, of which none are symmetric to y=-x
246 convex kites that are not parallelograms, of which 26 are symmetric to y=-x
32 rhombi, of which 6 are symmetric to y=-x
634 concave kites, of which 55 are symmetric to y=-x
3,806 concave trapezoids, of which none are symmetric to y=-x
78,630 convex general quadrilaterals, none of which are symmetric to y=-x
935,423 concave general quadrilaterals, none of which are symmetric to y=-x
If you want the number of solutions including those that are mirrors of any of the x solutions along the line y=x, the line y=-x or the origin, multiply the number of quadrilaterals that are symmetric to y=-x by 2 and the rest by 4 (because if a quadrilateral is symmetric to y=-x, then mirroring across the line y=-x yields the same quadrilateral and mirroring across the line y=x yields the same quadrilateral as mirroring across the origin)
If you cannot use both a and -a in the same solution, then there are 46,247 unique solutions:
12 rectangles
22 convex kites that are not parallelogramms
6 rhombi
66 concave kites
246 concave trapezoids
4,034 convex general quadrilaterals
41,861 concave general quadrilaterals
But on top of the 3 other solutions you get when mirroring along the identity line y=x, the negative identity line y=-x or the origin, quadrupling the number of solutions, you can double the number of solutions again because mirroring along the x-axis provides another solution for each of them. Note that mirroring along the x-axis didn’t always provide another solution when both a and -a are allowed: For example, mirroring (-9, -8),(-7, -6),(-5, 2),(-1, 1) along the x-axis results in (-9, 8),(-7, 6),(-5, -2),(-1, -1), where -1 was used twice.
*excludes
Here are, for example, the 32 rhombi, when a and -a are both allowed:
(-9, -8),(-6, -3),(-1, 0),(-4, -5),
(-9, -5),(-6, 0),(-1, 3),(-4, -2),
(-9, -3),(-6, 2),(-1, 5),(-4, 0),
(-9, -2),(-6, 3),(-1, 6),(-4, 1),
(-9, 0),(-6, -5),(-1, -8),(-4, -3),
(-9, 0),(-6, 5),(-1, 8),(-4, 3),
(-9, 3),(-6, -2),(-1, -5),(-4, 0),
(-9, 5),(-6, 0),(-1, -3),(-4, 2),
(-9, 6),(-6, 1),(-1, -2),(-4, 3),
(-9, 8),(-6, 3),(-1, 0),(-4, 5),
(-8, -7),(-5, -2),(0, 1),(-3, -4),
(-8, -4),(-5, 1),(0, 4),(-3, -1),
(-8, -2),(-5, 3),(0, 6),(-3, 1),
(-8, -1),(-5, 4),(0, 7),(-3, 2),
(-8, 1),(-5, -4),(0, -7),(-3, -2),
(-8, 4),(-5, -1),(0, -4),(-3, 1),
(-8, 6),(-5, 1),(0, -2),(-3, 3),
(-8, 7),(-5, 2),(0, -1),(-3, 4),
(-7, -6),(-4, -1),(1, 2),(-2, -3),
(-7, -3),(-4, 2),(1, 5),(-2, 0),
(-7, 2),(-4, -3),(1, -6),(-2, -1),
(-7, 5),(-4, 0),(1, -3),(-2, 2),
(-6, -5),(-3, 0),(2, 3),(-1, -2),
(-6, 3),(-3, -2),(2, -5),(-1, 0),
(-5, -4),(-2, 1),(3, 4),(0, -1),
(-5, 4),(-2, -1),(3, -4),(0, 1),
rhombi symmetric to y=-x:
(-9, 1),(-6, 6),(-1, 9),(-4, 4),
(-9, 9),(-6, 4),(-1, 1),(-4, 6),
(-7, -1),(-4, 4),(1, 7),(-2, 2),
(-7, 7),(-4, 2),(1, -1),(-2, 4),
(-6, -2),(-3, 3),(2, 6),(-1, 1),
(-6, 6),(-3, 1),(2, -2),(-1, 3),
And these are the 12 rectangles and the 6 rhombi, when a and -a are not both allowed:
rectangles:
(-7, 2),(-5, 0),(-1, 4),(-3, 6),
(-7, 4),(-5, 6),(-1, 2),(-3, 0),
(-8, 2),(-7, 3),(1, -5),(0, -6),
(-8, 3),(-6, 1),(-2, 5),(-4, 7),
(-8, 5),(-6, 7),(-2, 3),(-4, 1),
(-8, 5),(-7, 6),(1, -2),(0, -3),
(-9, 2),(-7, 0),(-3, 4),(-5, 6),
(-9, 2),(-8, 3),(0, -5),(-1, -6),
(-9, 4),(-7, 2),(-3, 6),(-5, 8),
(-9, 4),(-7, 6),(-3, 2),(-5, 0),
(-9, 5),(-8, 6),(0, -2),(-1, -3),
(-9, 6),(-7, 8),(-3, 4),(-5, 2),
rhombi:
(-8, 1),(-5, -4),(0, -7),(-3, -2),
(-8, 7),(-5, 2),(0, -1),(-3, 4),
(-9, 0),(-6, 5),(-1, 8),(-4, 3),
(-9, 3),(-6, -2),(-1, -5),(-4, 0),
(-9, 5),(-6, 0),(-1, -3),(-4, 2),
(-9, 8),(-6, 3),(-1, 0),(-4, 5)
The numbers for the version with digits from -9 to 9 (and both -a and a allowed in the same solution) are slightly incorrect because I exited the program I wrote (which calculated all solutions) too early. Also, some concave trapezoid were not recognized as such due to floating point errors and where thus incorrectly categorized as concave general quadrilaterals instead. Here are the corrected numbers:
86 rectangles, of which none are symmetric to y=-x
247 convex kites that are not parallelograms, of which 26 are symmetric to y=-x
32 rhombi, of which 6 are symmetric to y=-x
658 concave kites, of which 89 are symmetric to y=-x
9,758 concave trapezoids, of which none are symmetric to y=-x
78,661 convex general quadrilaterals, none of which are symmetric to y=-x
930,475 concave general quadrilaterals, none of which are symmetric to y=-x
In total: 1,019,917 solutions
Or
(86*4+221*4+26+569+9,858+78,661+930,475)*4+(26+6+89)*2 = 1,019,796*4 + 121*2 = 4,079,426 if you count all the quadrilaterals mirrored across the the identity line y=x, the negative identity line y=-x or the origin.
As you can see, the number of rectangles and rhombi didn’t change, so the solutions posted are still valid.
If you cannot use both a and -a in the same solution, then there are still 46,247 unique solutions, but (correcting that same floating point error from before):
516 concave trapezoids instead of 246 and only 41,591 concave general quadrilaterals instead of 41,861.
If the range of the digits is 0 to 9, then – instead of 2 concave trapezoids and 787 concave general quadrilaterals like claimed previously – there are 7 trapezoids and only 782 concave general quadrilaterals (that are not trapezoids or kites). The 5 concave trapezoids I mis-categorized as concave general quadrilaterals are:
(8, 5),(3, 0),(2, 7),(1, 6)
(9, 4),(2, 7),(5, 8),(0, 1)
(9, 5),(4, 0),(3, 7),(2, 6)
(9, 6),(4, 1),(3, 8),(2, 7)
(9, 8),(4, 1),(7, 2),(0, 5)