Open Middle®
Directions: Using the digits 1 to 9 at most one time each, fill in the boxes to make the largest sum.
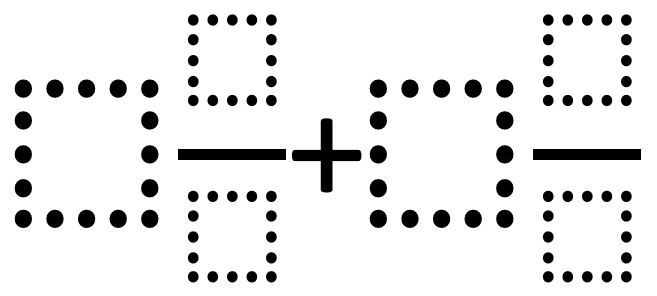
Hint
How can we make a really big fraction? If improper fractions are allowed, the numerators should be as big as possible and the denominators as small as possible.
Answer
The best I have found is 9 6/7 + 8 4/5 or 9 4/5 + 8 6/7. Otherwise 9 8/1 + 7 6/2 or 9 6/2 + 7 8/1 would be best, assuming improper fractions could be allowed.
Source: Robert Kaplinsky
No big deal, but I don’t think you’ve completely closed the end since 9 7/1 + 8 6/2 is the same (of course you can swap the order of the mixed numbers, too.)
You are totally right Jim. Thanks for adding to the discussion!
Also no big deal, but 9 4/5 + 8 6/7 is just as good as 9 6/7 + 8 4/5. Never hurts to emphasize that the whole number and fraction are added together, and addition’s commutative…
Actually it is a big deal Julie, you are absolutely right, thank you!
The way I read this was to multiply each whole number times the fraction first, then add the two terms. This adds a little twist, but works out to the same answer of 9(8/1) + 7(6/2) for a total of 93.
Interesting approach, but with the title it is assumed they are adding mixed numbers. Thank you for your response!
Smallest sum:
1 3/8 + 2 4/9 = 3.8194
Greatest sum:
Allowing improper fractions in mixed numbers:
7 6/2 + 8 9/1 = 27.0
7 6/2 + 9 8/1 = 27.0
8 6/2 + 9 7/1 = 27.0
Not allowing improper fractions in mixed numbers:
8 4/5 + 9 6/7 = 18.6571
Note: Each of the results given can also be obtained by swapping the fractional parts or the whole parts of the mixed numbers, each of the two swaps multiplying the number of solutions by 2. So 27 can actually be gotten in 3 * 2 * 2 = 12 ways.
97/8+64/5