Directions: Using the integers 1 to 10 at most one time each, fill in the boxes so that the sum is equal to 1.
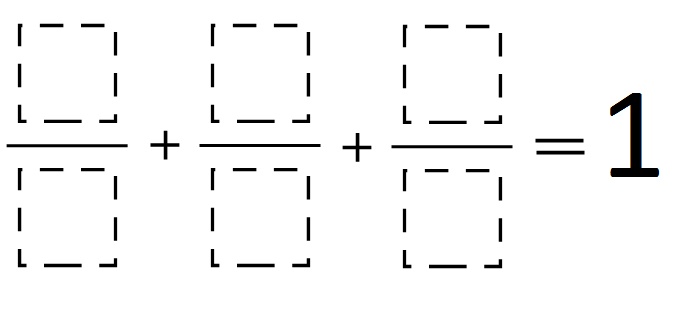
Hint
What three unit fractions add up to exactly 1 whole? What numbers would you use for the denominators? Why?
Answer
There are many solutions. Here are some possible solutions:
1/6 + 4/8 + 3/9
3/6 + 2/8 + 1/4
1/6 + 4/8 + 3/9
3/6 + 2/8 + 1/4
Source: Joshua Nelson
 Open Middle®
Open Middle®



Our class came up with two different solutions:
1.) 1/4 + 2/8 + 5/10
2.) 3/6 + 1/4 + 2/8
Sorry, I forget it.is “2.)”
all 48 solutions
1/4 + 2/8 + 3/6= 1
1/4 + 2/8 + 5/10= 1
1/4 + 3/6 + 2/8= 1
1/4 + 5/10 + 2/8= 1
1/5 + 2/4 + 3/10= 1
1/5 + 3/10 + 2/4= 1
1/5 + 3/10 + 4/8= 1
1/5 + 4/8 + 3/10= 1
1/6 + 2/4 + 3/9= 1
1/6 + 3/9 + 2/4= 1
1/6 + 3/9 + 4/8= 1
1/6 + 3/9 + 5/10= 1
1/6 + 4/8 + 3/9= 1
1/6 + 5/10 + 3/9= 1
1/10 + 2/5 + 3/6= 1
1/10 + 2/5 + 4/8= 1
1/10 + 3/6 + 2/5= 1
1/10 + 4/8 + 2/5= 1
2/4 + 1/5 + 3/10= 1
2/4 + 1/6 + 3/9= 1
2/4 + 3/10 + 1/5= 1
2/5 + 1/10 + 3/6= 1
2/5 + 1/10 + 4/8= 1
2/5 + 3/6 + 1/10= 1
2/5 + 4/8 + 1/10= 1
2/8 + 1/4 + 3/6= 1
2/8 + 1/4 + 5/10= 1
2/8 + 3/6 + 1/4= 1
2/8 + 5/10 + 1/4= 1
3/6 + 1/4 + 2/8= 1
3/6 + 1/10 + 2/5= 1
3/6 + 2/5 + 1/10= 1
3/6 + 2/8 + 1/4= 1
3/9 + 1/6 + 2/4= 1
3/9 + 1/6 + 4/8= 1
3/9 + 1/6 + 5/10= 1
3/10 + 1/5 + 2/4= 1
3/10 + 1/5 + 4/8= 1
3/10 + 2/4 + 1/5= 1
3/10 + 4/8 + 1/5= 1
4/8 + 1/5 + 3/10= 1
4/8 + 1/6 + 3/9= 1
4/8 + 1/10 + 2/5= 1
4/8 + 2/5 + 1/10= 1
4/8 + 3/10 + 1/5= 1
5/10 + 1/4 + 2/8= 1
5/10 + 1/6 + 3/9= 1
5/10 + 2/8 + 1/4= 1
All 48 solutions reduce to 9 unique solutions. (ignore the order)
a/b+c/d+e/f=1
let a<c<e, done.
1/4 + 2/8 + 3/6= 1
1/4 + 2/8 + 5/10= 1
1/5 + 2/4 + 3/10= 1
1/5 + 3/10 + 4/8= 1
1/6 + 2/4 + 3/9= 1
1/6 + 3/9 + 4/8= 1
1/6 + 3/9 + 5/10= 1
1/10 + 2/5 + 3/6= 1
1/10 + 2/5 + 4/8= 1
If a/b + c/d + e/f = 1, then the following 6 equations (obtained by swapping summands (fractions) around, multiplying the number of solutions by 6) are also true:
a/b + c/d + e/f = 1
c/d + a/b + e/f = 1
a/b + e/f + c/d = 1
c/d + e/f + a/b = 1
e/f + c/d + a/b = 1
e/f + a/b + c/d = 1
So for each solution, there are 5 equivalent ones, multiplying the number of solutions by 6.
So there are 9 * 6 = 54 solutions that reduce down to these 9 unique ones.
Your list of “all” 48 solutions…
… has 2/4 + 1/6 + 3/9= 1, but is missing 2/4 + 3/9 + 1/6= 1
… has 3/9 + 1/6 + 2/4= 1, but is missing 3/9 + 2/4 + 1/6= 1
… has 3/9 + 1/6 + 4/8= 1, but is missing 3/9 + 4/8 + 1/6= 1
… has 3/9 + 1/6 + 5/10= 1, but is missing 3/9 + 5/10 + 1/6= 1
… has 4/8 + 1/6 + 3/9= 1, but is missing 4/8 + 3/9 + 1/6= 1
… has 5/10 + 1/6 + 3/9= 1, but is missing 5/10 + 3/9 + 1/6= 1
With these additional 6 solutions, you get all the 54 solutions.