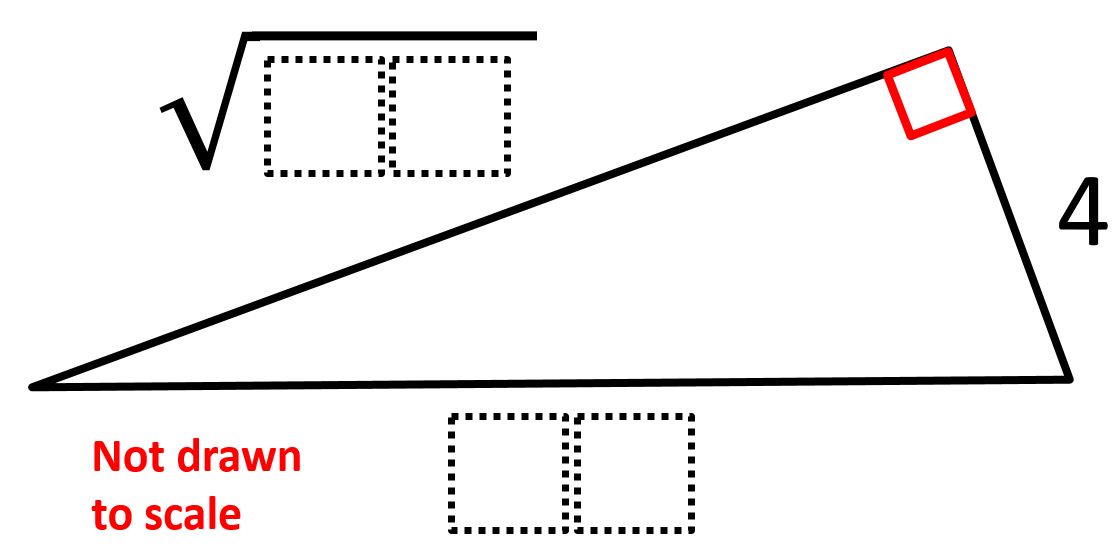
Directions: Using the digits 0 to 9, at most one time each, fill in the boxes to find the lengths of the missing sides such that the missing leg’s length is as long as possible.
Hint
How do we figure out the length of the remaining side?
Which side of a right triangle is the longest?
Answer
So, the possible side lengths for the triangles are (a, b, and c being the leg, leg, and hypotenuse):
a, b, c
4, √84, 10
4, √65, 09
4, √48, 08
4, √33, 07
4, √20, 06
4, 03, 05
After removing the solutions that duplicate digits, you are left with only two options:
a, b, c
4, √65, 09 (from Karl S.)
4, √84, 10
Therefore, 4, √84, 10 is the optimal solution. Be on the lookout though for students who make the leg longer than the hypotenuse. While we want the missing leg to be as long as possible, it still has to be less than the length of the hypotenuse. So, this is a good chance to check for misunderstandings.
Source: Robert Kaplinsky
 Open Middle®
Open Middle®



Love it!
Same!
4 and 84 share a digit of 4. Shouldn’t that response be eliminated, too?
The reason that is not eliminated is because 4 is given. There is just no repeating of the numbers you use, not including ones that are given.
Ok, got it! Thanks for the swift reply.
Couldn’t 4, sqrt(65), and 09 also be a possible solution, albeit not as long as your given optimal solution?
You are totally right Karl. I’ve updated the answer accordingly.
I don’t really understand
We found another solution. We used the square root of 93 for the leg and got 10.4 for the hypotenuse, so we used the numbers 9, 3, 1, and 0.